A uniform ladder of mass $10 k g$ leans against a smooth vertical wall making an angle $53^{0}$ with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder.

Text Solution

Verified by Experts

The ladder is in equilibrium
$∴ N_{1} = f$ and
$N_{2} = W$
Taking torque about .B.
$N_{1} (A O) = W (C B)$ .
or $N_{1} (A B) cos 53 = W (\frac{A B}{2}) sin 53$
or $N_{1} = \frac{2}{3} W$
and $N_{2} = W = 10 \times 9.8 = 98 N$
The frictional force is
$f = N_{1} = \frac{2}{3} W = 65 N$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
In the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle $θ$ with the horizontal floor. The coefficient of friction between the wall and the ladder is $μ_{1}$ and that between the floor and the ladder is $μ_{2} .$ the normal reaction of the wall on the ladder is $N_{1}$ and that of the floor is $N_{2} .$ if the ladder is about to slip. than

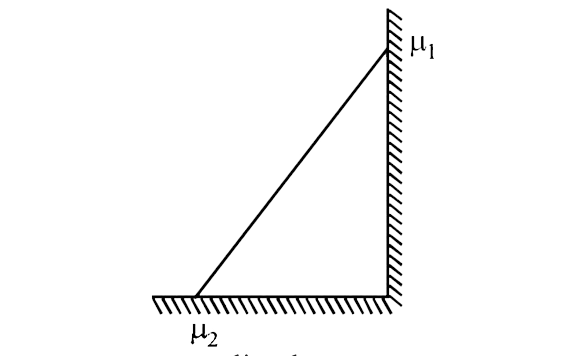A $μ_{1} = 0, μ_{2} \neq and N_{2} tan θ = \frac{m g}{2}$
B $μ_{1} \neq 0, μ_{2} = 0 and N_{1} tan θ = \frac{m g}{2}$
C $μ_{1} \neq 0, μ_{2} \neq 0 and N_{2} = \frac{m g}{1 + μ_{1} μ_{2}}$
D $μ_{1} = 0, μ_{2} \neq 0 and N_{1} tan θ = \frac{m g}{2}$

AAKASH SERIES-SYSTEM OF PARTICLES AND ROTATIONAL MOTION-Problems

Home
Ask Doubt
Profile