A capacitor of capacitance C1=1.0μF charged upto a voltage V=110V is connected in parallel to the terminals of a circuit consisting of two uncharged capacitors connected in series and possessing the capacitance C2=2.0μF and C3=3.0μF. What charge will flow through the connecting wires?
The correct Answer is:C
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the initial charge on capacitor C1
The charge Q1 on capacitor C1 can be calculated using the formula:
Q1=C1×V
Where:
- C1=1.0μF=1.0×10−6F
- V=110V
Substituting the values:
Q1=1.0×10−6F×110V=1.1×10−4C=110μC
Step 2: Find the equivalent capacitance of capacitors C2 and C3 in series
The equivalent capacitance Ceq for capacitors in series is given by:
1Ceq=1C2+1C3
Where:
- C2=2.0μF=2.0×10−6F
- C3=3.0μF=3.0×10−6F
Calculating Ceq:
1Ceq=12.0×10−6+13.0×10−6=3+26×106=56×106
Thus,
Ceq=65×10−6F=1.2μF
Step 3: Apply charge conservation in the parallel circuit
When C1 is connected in parallel with the equivalent capacitance Ceq, the total charge Qtotal is conserved:
Q1=Qeq+QC1
Where QC1 is the charge on C1 after connecting to the uncharged capacitors.
Step 4: Relate the charges using the capacitance values
Since both capacitors are in parallel, the voltage across them will be the same:
V=QC1C1=QeqCeq
From this, we can express QC1 in terms of Qeq:
QC1=C1×VandQeq=Ceq×V
Step 5: Set up the equations
From the conservation of charge:
Q1=QC1+Qeq
Substituting QC1 and Qeq:
110μC=C1CeqQeq+Qeq
This simplifies to:
110μC=(C1+CeqCeq)Qeq
Step 6: Solve for Qeq
Substituting C1=1.0μF and Ceq=1.2μF:
110μC=(1.0+1.21.2)Qeq
110μC=(2.21.2)Qeq
Qeq=110×1.22.2μC=60μC
Final Answer
The charge that flows through the connecting wires is Qeq=60μC.
---
Q1=C1×V
Where:
- C1=1.0μF=1.0×10−6F
- V=110V
Q1=1.0×10−6F×110V=1.1×10−4C=110μC
1Ceq=1C2+1C3
Where:
- C2=2.0μF=2.0×10−6F
- C3=3.0μF=3.0×10−6F
1Ceq=12.0×10−6+13.0×10−6=3+26×106=56×106
Thus,
Ceq=65×10−6F=1.2μF
Q1=Qeq+QC1
Where QC1 is the charge on C1 after connecting to the uncharged capacitors.
V=QC1C1=QeqCeq
QC1=C1×VandQeq=Ceq×V
Q1=QC1+Qeq
Substituting QC1 and Qeq:
110μC=C1CeqQeq+Qeq
This simplifies to:
110μC=(C1+CeqCeq)Qeq
110μC=(1.0+1.21.2)Qeq
110μC=(2.21.2)Qeq
Qeq=110×1.22.2μC=60μC
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
C1=5.6μF is charged upto 220V. Another capacitor C2=2.8μF is connected in parallel. Find loss in energy ?
View SolutionA capacitor of capacitance 1μF is charged to a potential of 1V, it is connected in parallel to an inductor of inductance 10−3H. The maximum current that will flow in the circuit has the value
View Solution
Knowledge Check
- Question 1 - Select One
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
A capacitor of capacity 2μF is charged to 100V. What is the heat generated when this capacitor is connected in parallel to an another capacitor of same capacity?
View SolutionA capacitor of 20μF charged upto 500 V is connected in parallel with another capacitor of 10μF, which is charged upto 200 V. the common potential is
View SolutionA capacitorn of 2μF charged to 50 V is connected in parallel with another capacitor of 1μF charged to 20 V. The common potential and loss of energy will be
View SolutionA capacitor of capacity 20microF is charged upto 500V and and disconnected from cell. Now this charged capacitor is connected to another capacitor of capacitance C If final common potential is 20V then find the capacitance C.
View SolutionA capacitor C1=1.0μF is charged up to a voltage V=60 V by connecting it to battery B through switch (1) Now C1 is disconnected from battery and connected to a circuit consisting of two uncharged capaictors C2=3.0μFandC3=6.0μF through switch (2) as shown in the figure The sum of final charges on C2andc3 is :
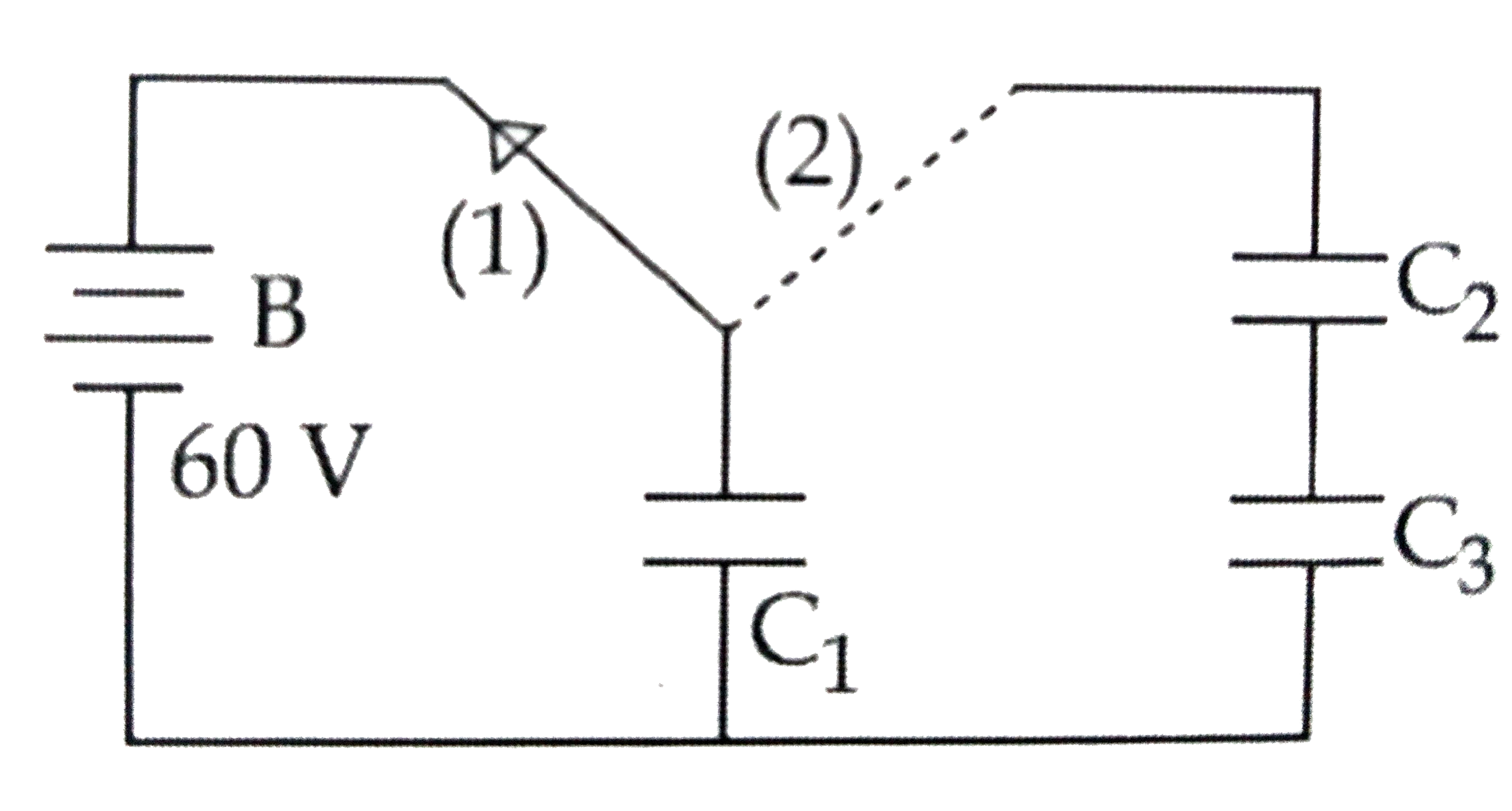 View Solution
View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionA capacitor of 0.75μF is charged to a voltage of 16 V. What is the magnitude of the charge on each plate of the capacitor ?
View Solution

