कथन - I : n−1∑r=01n(√rn+1)<∫10(√x+1)dx<n∑r=11n(√rn+1),n∈N
क्योकि
कथन - II : यदि f(x) अन्तराल [0,1] में संतत् तथा वर्धमान है, तो n−1∑r=01n(rn)<∫10f(x)dx<n∑r=11nf(rn) , जहाँ n∈N
कथन - I सत्य है, कथन - II सत्य है, कथन - II, कथन - I का सही स्पष्टीकरण है।
कथन - I सत्य है, कथन - II सत्य है, कथन - II, कथन - I का सही स्पष्टीकरण नहीं है।
कथन - I सत्य है,परन्तु कथन - II असत्य है
कथन - I असत्य है,परन्तु कथन - II सत्य है
The correct Answer is:A
Step by step video, text & image solution for कथन - I : sum _( r = 0) ^( n - 1) (1)/( n) ( sqrt(( r)/( n)) + 1) lt int _(0) ^(1) ( sqrt( x) + 1) dx lt sum _( r = 1) ^( n) (1)/( n) ( sqrt(( r)/( n) + 1) ) , n in N क्योकि कथन - II : यदि f(x) अन्तराल [0,1] में संतत् तथा वर्धमान है, तो sum _( r = 0) ^( n - 1) (1)/( n) (( r)/(n)) lt int_(0) ^(1) f (x) dx lt sum _( r = 1) ^( n) (1)/( n) f (( r)/( n)) , जहाँ n in N by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - DEFINITE INTEGRATIONEXERCISE - Exercise - 03 (गद्यांश आधारित प्रश्न) गद्यांश 13videos
DEFINITE INTEGRATION
- BOOK - ALLEN HINDICHAPTER - DEFINITE INTEGRATIONEXERCISE - Exercise - 03 (गद्यांश आधारित प्रश्न) गद्यांश 23videos
DEFINITE INTEGRATION
- BOOK - ALLEN HINDICHAPTER - DEFINITE INTEGRATIONEXERCISE - Exercise - 03 (स्तम्भ सुमेलन)3videos
DEFINITE INTEGRATION
- BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -05 [B] (JEE-ADVANCED: PREVIOUS YEAR QUESTIONS)2videos
CONTINUITY
- BOOK - ALLEN HINDICHAPTER - DETERMINANTEXERCISE - DO YOURSELF -91videos
DETERMINANT
Similar Questions
माना g(x)=∫x0f(t)dt, जहाँ f एक फलन है जिसका आरेख दर्शाया गया है।
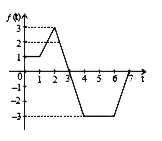
x∈[0,7] में g (x) का अधिकतम मान होगा -08:08View Solutionफलन f (x) का अन्तराल [ a, b] में, औसत मान संख्या μ=1b−a∫baf(x)dx है |
{1b−a∫ba[f(x)]2dx}1/2 को [a, b] में f का वर्ग माध्य मूल मान कहते है। μ औसत मान प्राप्त करेगा यदि f, [ a, b] का संतत् हो।
अन्तराल [0,π] पर y = sin x की औसत कोटि है -04:24View Solutionनिम्न प्रश्न में दो स्तम्भ में वत्क्व्य (statements) दिये गए है जिनका सम्मेलन (match) करना है । स्तम्भ - I(Column-I) के वत्क्व्यो को A, B, C तथा D नामित किया गया है जबकि स्तम्भ -II - (Column-II) के वत्क्व्यो को p,q, r तथा s नामित किया ज्ञात है। स्तम्भ- I (Column-I ) में दिए गए कोई एक वत्क्व्य स्तम्भ -II (Column-II ) के एक वत्क्व्य से सही सुमेल करता है।
 03:07View Solution
03:07View Solutionफलन f(x)=⎧⎨⎩e1/x−1e1/x+1जबx≠01जबx=0 का x=0 पर सततता का परीक्षण कीजिए।
04:25View Solutionसमीकरण निकाय λx+y+z=0,−x+λy+z=0,−x−y+λz=0 का एक अशून्य हल होगा यदि λ का वास्तविक मान है
06:59View Solutionn∑r=1sin−1(√r−√r−1√r(r+1))is equal to
(a) tan−1(√n)−π4
(b)tan−1(√n+1)−π4
(c)tan−1(√n)
(d) tan−1(√n+1)06:58View SolutionIf Cr=n![r!(n−r)], the prove that √C1+√C2+.......√Cn<√n(2n−1)<√n(2n−1).<>="">
View SolutionIf a_(n)=sum((1)/(C)(n,r) from r=0 to n, then sum((r)/(C)(n,r))
04:59View SolutionStatement -2: n∑r=0(−1)rnCrr+1=1n+1
Statement-2: n∑r=0(−1)rnCrr+1xr=1(n+1)x{1−(1−x)n+1}01:55View SolutionProve that :
(i) n!r!=n(n−1)(n−2)...(r+1)
(ii) (n−r+1)⋅n!(n−r+1)!=n!(n−r)!
(iii) n!r!(n−r)!+n!(r−1)!(n−r+1)!=(n+1)!r!(n−r+1)!02:53View SolutionThe value of limn→∞n∑r=11n√(n+rn−r) is :
03:37View Solutionlimx→∞n−1∑r=1√n+rn2(n−r)=
04:45View SolutionLtn→∞1n2n∑r=1r√n2+r2=
03:32View SolutionLtn→∞1nn∑r=1√rn=
05:35View SolutionIf Cr=n![r!(n−r)], the prove that √C1+√C2+.......√Cn<√n(2n−1)<√n(2n−1).<>="">
05:55View Solution

