A bullet of mass 5gm is fired horizontally into block of mass 1kg at rest on a horizontal surface and gets embedded in it. The combination moves 5m before coming to rest. If μk=0.40, what is the speed with which the bullet strikes the block ?
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have a bullet of mass mb=5g=0.005kg that is fired horizontally into a block of mass mB=1kg at rest. After the bullet embeds itself in the block, they move together and come to rest after traveling a distance of d=5m. The coefficient of kinetic friction between the block and the surface is μk=0.40. We need to find the speed v with which the bullet strikes the block.
Step 2: Use Conservation of Momentum
When the bullet embeds itself in the block, we can apply the conservation of momentum:
mbv=(mb+mB)v′
Here, v′ is the velocity of the combined system (bullet + block) immediately after the collision.
Step 3: Calculate the Velocity After Collision
The mass of the bullet is negligible compared to the mass of the block, so we can approximate:
v′≈mbvmB
Step 4: Use Work-Energy Principle
The work done by friction as the block moves a distance d is equal to the initial kinetic energy of the system just after the collision:
Work done by friction=μk(mb+mB)gd
The initial kinetic energy of the system is:
K.E.=12(mb+mB)v′2
Setting these equal gives us:
μk(mb+mB)gd=12(mb+mB)v′2
Step 5: Simplify the Equation
We can cancel (mb+mB) from both sides (since it's non-zero):
μkgd=12v′2
Step 6: Solve for v′
Rearranging gives:
v′2=2μkgd
Taking the square root:
v′=√2μkgd
Step 7: Substitute Values
Now, substituting μk=0.40, g=10m/s2, and d=5m:
v′=√2⋅0.40⋅10⋅5
Calculating this gives:
v′=√40=2√10m/s
Step 8: Substitute Back to Find v
Now we can substitute v′ back into the momentum equation to find v:
v=(mb+mB)v′mb=(0.005+1)⋅2√100.005
Calculating this gives:
v≈400√10m/s
Final Answer
Thus, the speed with which the bullet strikes the block is approximately 400√10m/s.
---
We have a bullet of mass mb=5g=0.005kg that is fired horizontally into a block of mass mB=1kg at rest. After the bullet embeds itself in the block, they move together and come to rest after traveling a distance of d=5m. The coefficient of kinetic friction between the block and the surface is μk=0.40. We need to find the speed v with which the bullet strikes the block.
When the bullet embeds itself in the block, we can apply the conservation of momentum:
The mass of the bullet is negligible compared to the mass of the block, so we can approximate:
The work done by friction as the block moves a distance d is equal to the initial kinetic energy of the system just after the collision:
We can cancel (mb+mB) from both sides (since it's non-zero):
Rearranging gives:
Now, substituting μk=0.40, g=10m/s2, and d=5m:
Now we can substitute v′ back into the momentum equation to find v:
Thus, the speed with which the bullet strikes the block is approximately 400√10m/s.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Additional solved examples9videos
FRICTION
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Conceptual short answer questions with answer9videos
FRICTION
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS12videos
DYNAMICS
- BOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP2videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass 25 g is fired horizontally into a ballistic pendulum of mas 5.0 kg and gets embedded in it figure. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View SolutionA bullet of mass 10 g is fired horizontally into a 4 kg wooden block resting on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.25. The bullet is embadded the block and the combination moves a distance of 20 m before coming to rest. Find the speed of the bullet just before striking the block. (g=10m/s2)
View SolutionA force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
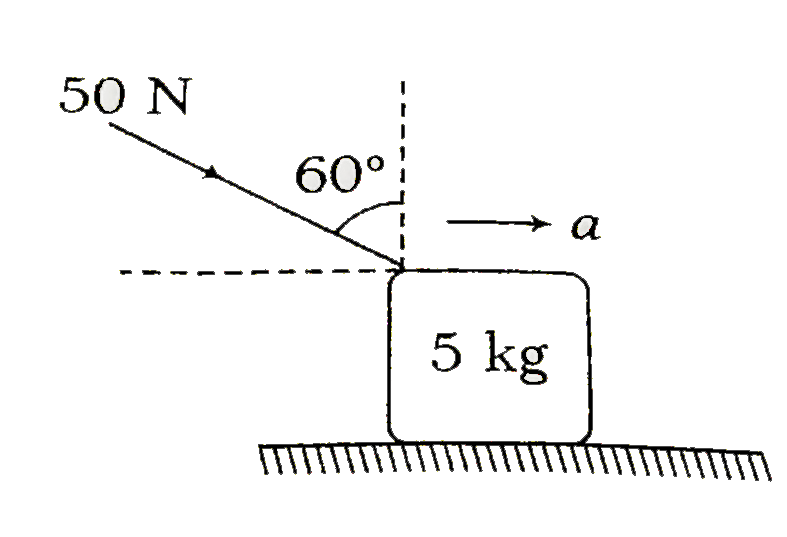 View Solution
View SolutionA force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
 View Solution
View SolutionA block of mass 2 kg rests on a horizontal surface. If a horizontal force of 5 N is applied on the block, the frictional force on it is (take,uk=0.4,μs=0.5)
View Solution

