Doubtnut Promotions Sticky

A force acts on a particle moving at a relativistic speed in a direction perpendiculal' to its path. How will the particle move? Express the force in terms of the speed and of the radius of curvature of the path.

Text Solution
Verified by Experts

The correct Answer is:The particle moves in a circle. The expression for the force will be formally the same as in Newtonian mechanics.

Since the force is perpendicular to the path, the magnitude of the momentum does not change (Fig. 6.13). | p 1 | = | p 2 | = p .Tne maghudae of the momentum.s variation is ) Δ p = p | Δ ϕ | . The normal force is
F n = | Δ p | Δ t = p | Δ ϕ | Δ t = p ω =
= m ω 2 r = m v 2 r
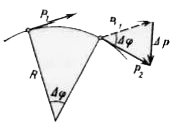
ocr_image
Formally, we have obtained the Fig. 6.13 same result as in the case of the nonrelativistic motion of a particle in a circular path (see 7.2). However, in the relativistic case the expression for the force contains the relativistic mass. Thus, in the particular case the force is perpendicular to the path) the relativistic approach produces formally ihe same result as the classical approach, although in general the second law of Newton in the form F=ma is not valid for relativistic motion.

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 12PHYSICSDUAL NATURE OF RADIATION AND MATTER

Similar Questions

Knowledge Check

  • Question 1 - Select One

    If the speed of a particle moving at a relativistic speed is doubled, its linear momentum will

    ABecome double
    Bbocome more than double
    Cremain equal
    Dbecome less than double.
  • Question 2 - Select One

    A charged particle is moving in a uniform magnetic field and losses 4% of its KE. The radius of curvature of its path change by

    A0.02
    B0.04
    C0.1
    DNone of these
  • Question 3 - Select One

    A particle is moving with a constant speed along a straight line path. A force is not required to

    AIncrease its speed
    BDecrease the momentum
    CChange the direction
    DKeep it moving with uniform velocity