The electrostatic potential energy of two point charges, 1μC each, placed 1 metre apart in air is :
9×103J
9×109J
9×10−3J
9×10−3J
The correct Answer is:c
To find the electrostatic potential energy (U) of two point charges, we can use the formula:
U=k⋅q1⋅q2r
Where:
- U is the electrostatic potential energy,
- k is Coulomb's constant (9×109N m2/C2),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
1. Identify the values:
- Both charges q1 and q2 are 1μC=1×10−6C.
- The distance r between the charges is 1m.
- The value of k is 9×109N m2/C2.
2. Substitute the values into the formula:
U=9×109⋅(1×10−6)⋅(1×10−6)1
3. Calculate the product of the charges:
(1×10−6)⋅(1×10−6)=1×10−12
4. Substitute this back into the equation:
U=9×109⋅1×10−121
5. Perform the multiplication:
U=9×10−3J
6. Final result:
The electrostatic potential energy of the two point charges is:
U=0.009Jor9mJ
- U is the electrostatic potential energy,
- k is Coulomb's constant (9×109N m2/C2),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
- Both charges q1 and q2 are 1μC=1×10−6C.
- The distance r between the charges is 1m.
- The value of k is 9×109N m2/C2.
U=9×109⋅(1×10−6)⋅(1×10−6)1
(1×10−6)⋅(1×10−6)=1×10−12
U=9×109⋅1×10−121
U=9×10−3J
The electrostatic potential energy of the two point charges is:
U=0.009Jor9mJ
Similar Questions
(a) Determine the electrostatic potential energy of a system consisting of two charge 7μCand−2μC (and with no external field) placed at (−9cm,0,0)and(9cm,0,0) respectively.
(b) How much work is required to seperate the two charges infinitely away from each other ?
(c) Suppose that the same system of charges is now placed in an external electric field E=A×1/r2, where A=9×105Cm−2.
What would the electrostatic energy of the configuration be ?
View SolutionCalculate electrostatic potential energy stored in a system consisting of two point charges 100μC and 40μC separated by a distance of 9cm, in vacuum.
View SolutionThe electrostatic potential energy between proton and electron separated by a distance 1 Å is
View SolutionTwo point charges 4Q, Q are separated by 1m in air. At what point on the line joining the charges is the electric field intensity zero ?
Also calculate the electrostatic potential energy of the system of charges, taking the value of charge, Q=2×10−7C.
View SolutionTwo point charges of +Q each have been placed at the positions (−a/2,0,0)and(a/2,0,0).The locus of the points where - Q charge can be placed such the that total electrostatic potential energy of the system can become equal to zero, is represented by which of the following equations ?
View SolutionIs it possible to have an arrangement of two point charges separated by finite distances such that the electric potential energy of the arrangement is the same as if the two charges were infinitely far apart? What if there are three charges?
View SolutionThe electrostatic potential due to the charge configuration at point P as shown in figure for b << a is
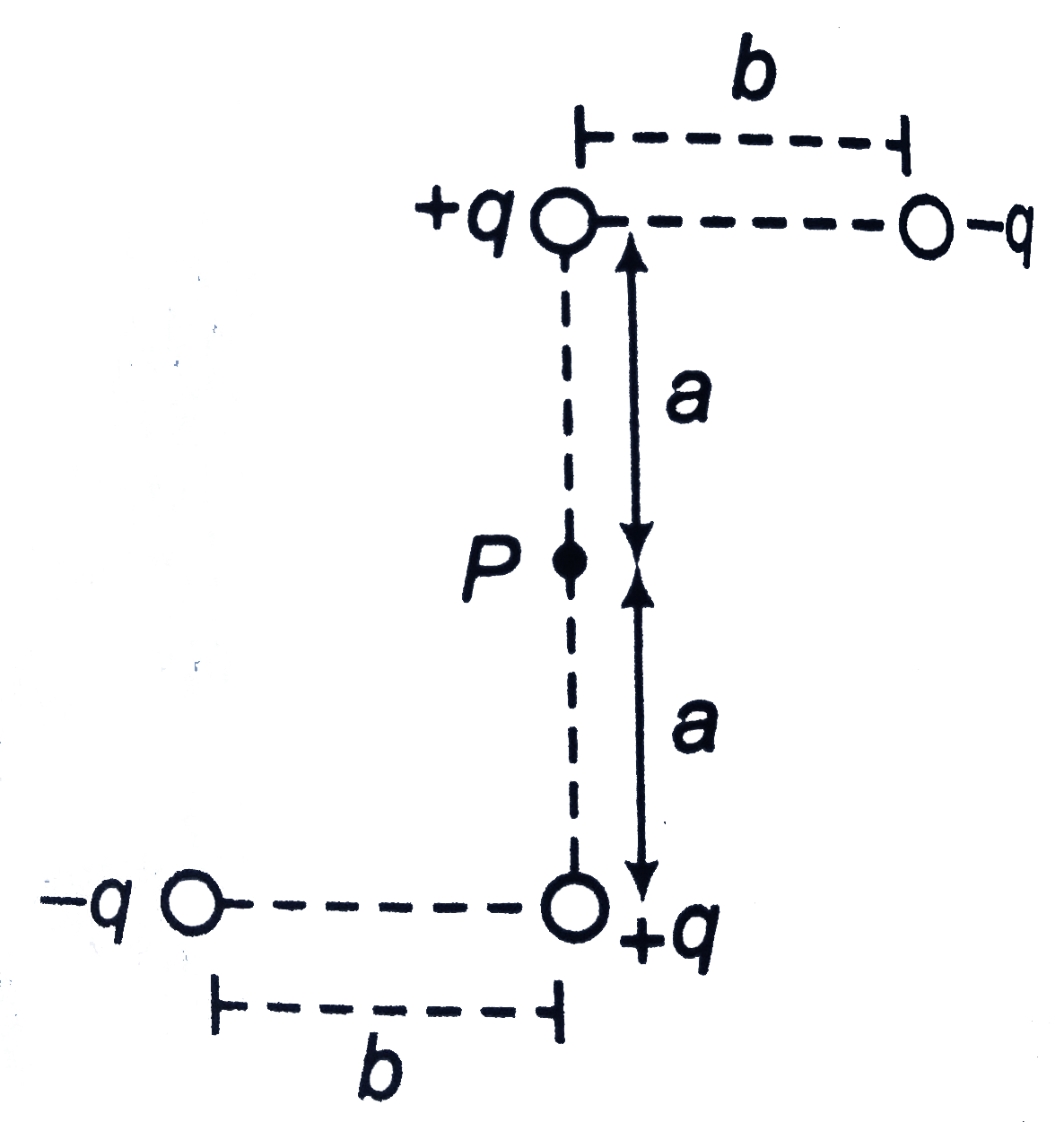
View SolutionAssertion : When two positive point charges move away from each other, then their electrostatic potential energy decreases.
Reason : Change in potential energy between two points is equal to the work done by electrostatic forces.
View SolutionFind out the electrostalic force between two point charges placed in air (each of +1 C) if they are separately by 1 m.
View SolutionA point charge q1=4.00nC is placed at the origin, and a second point charge q2=−3.00nC, placed on the x-axis at x = + 20.0 cm. A third point charge q3=2.00nC is placed on the X-axis between q1,andq2. (Take as zero the potential energy of the three charges when they are infinitely far apart).
(a) What is the potential energy of the system of the three charges if q3 is placed at x= + 10.0 cm?
(b) Where should q3 be placed to make the potential energy of the system equal to zero?
View Solution
