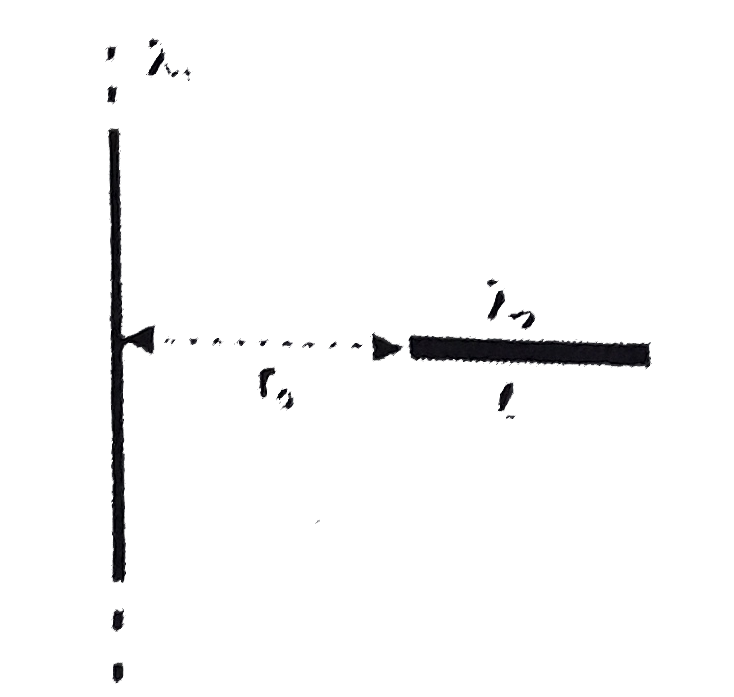
A segment of a charged wire of length l, charge density λ2 and an infinitely long charged wire. Charge density λ1. Lie in a plate at right angles to each other. The separation between the wires is r0. Determine the force of interction between the wires.
To solve the problem of determining the force of interaction between a segment of a charged wire and an infinitely long charged wire, we can follow these steps:
Step 1: Understand the Configuration
We have two wires:
- Wire 1: An infinitely long wire with charge density λ1.
- Wire 2: A segment of length l with charge density λ2, positioned perpendicular to Wire 1 at a distance r0.
Step 2: Calculate the Electric Field due to Wire 1
The electric field E produced by an infinitely long charged wire at a distance r from the wire is given by the formula:
E=λ12πϵ0r
where ϵ0 is the permittivity of free space.
Step 3: Consider a Small Element of Wire 2
To find the force on Wire 2 due to the electric field from Wire 1, we consider a small segment dx of Wire 2 at a distance x from Wire 1. The charge dq on this segment can be expressed as:
dq=λ2dx
Step 4: Calculate the Force on the Small Segment
The force dF acting on the small segment dx of Wire 2 due to the electric field E from Wire 1 is given by:
dF=dq⋅E=λ2dx⋅λ12πϵ0x
Thus,
dF=λ1λ22πϵ0xdx
Step 5: Integrate to Find the Total Force
To find the total force F on Wire 2, we integrate dF from r0 to r0+l:
F=∫r0+lr0dF=∫r0+lr0λ1λ22πϵ0xdx
Step 6: Perform the Integration
The integral of 1x is ln(x), so we have:
F=λ1λ22πϵ0(ln(x))r0+lr0
This evaluates to:
F=λ1λ22πϵ0(ln(r0+l)−ln(r0))
Step 7: Simplify the Expression
Using the properties of logarithms, we can simplify this to:
F=λ1λ22πϵ0ln(r0+lr0)
Final Result
The force of interaction between the wires is given by:
F=λ1λ22πϵ0ln(r0+lr0)
We have two wires:
- Wire 1: An infinitely long wire with charge density λ1.
- Wire 2: A segment of length l with charge density λ2, positioned perpendicular to Wire 1 at a distance r0.
The electric field E produced by an infinitely long charged wire at a distance r from the wire is given by the formula:
E=λ12πϵ0r
where ϵ0 is the permittivity of free space.
To find the force on Wire 2 due to the electric field from Wire 1, we consider a small segment dx of Wire 2 at a distance x from Wire 1. The charge dq on this segment can be expressed as:
dq=λ2dx
The force dF acting on the small segment dx of Wire 2 due to the electric field E from Wire 1 is given by:
dF=dq⋅E=λ2dx⋅λ12πϵ0x
Thus,
dF=λ1λ22πϵ0xdx
To find the total force F on Wire 2, we integrate dF from r0 to r0+l:
F=∫r0+lr0dF=∫r0+lr0λ1λ22πϵ0xdx
The integral of 1x is ln(x), so we have:
F=λ1λ22πϵ0(ln(x))r0+lr0
This evaluates to:
F=λ1λ22πϵ0(ln(r0+l)−ln(r0))
Using the properties of logarithms, we can simplify this to:
F=λ1λ22πϵ0ln(r0+lr0)
The force of interaction between the wires is given by:
F=λ1λ22πϵ0ln(r0+lr0)
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples
10 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
An infinitely long string uniformly charged with a linear charge density λ1 and a segment of length l uniformly charge with linear charge density λ2 lie in a plane at right angles to each other and separated by a distance r0 as shown in figure. The force with which these two interact is λ1λ24πε0ln(x). If l=r0, then find the value of x.
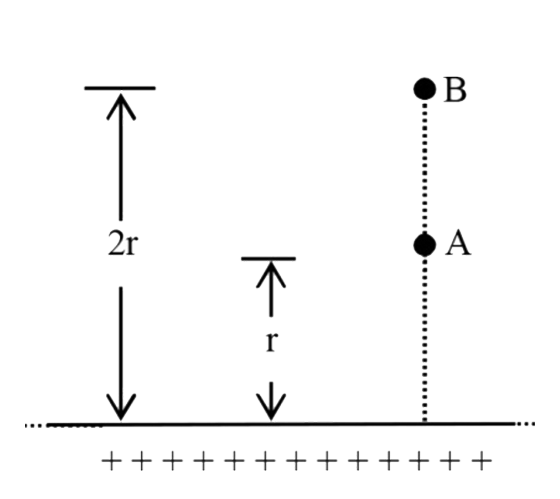
View SolutionAn infinitely long line of linear charge density λ is shown in the figure. The potential difference VA−VB between the two points A and B is
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
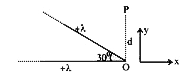
View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
View SolutionTwo infinitely long thin straight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionTwo parallel infinite line charges +λand−λ are placed with a separation distance R in free space. The net electric field exactly mid-way between the two line charges is
View SolutionTwo parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
View SolutionTwo uniformly long charged wires with linear densities λ and 3λ are placed along X and Y axis respectively. Determined the slope of electric field at any point on the l ine y=√3x
View SolutionFind the electric flux crossing the wire frame ABCD of length l, width b, and center at a distance OP = d from an infinite line of charge with linear charge density λ. Consider that the plane of the frame is perpendicular to the line OP

View Solution
