Prove that the lowering of the stabilised orbitals is 0.4Δ0 while raising of the destabilised orbitalsw is 0.6Δ0 .
To prove that the lowering of the stabilized orbitals is 0.4Δ0 while the raising of the destabilized orbitals is 0.6Δ0, we will use the concepts from Crystal Field Theory (CFT).
1. Understanding the Splitting of d-Orbitals:
- In a coordination compound, the five d-orbitals split into two sets due to the electrostatic interactions with surrounding ligands: the lower-energy set T2g (comprising dxy, dyz, and dzx) and the higher-energy set Eg (comprising dx2−y2 and dz2).
2. Defining Energies:
- Let X be the energy of stabilization for the T2g orbitals and Y be the energy of destabilization for the Eg orbitals.
- The total energy of separation due to the ligand field is denoted as Δ0.
3. Setting Up the Equations:
- From the theory, we have the relationship:
Y−X=Δ0(1)
- The total stabilization energy for the T2g orbitals (3 orbitals) and destabilization for the Eg orbitals (2 orbitals) can be expressed as:
3X−2Y=0(2)
4. Solving the Equations:
- From equation (1), we can express Y in terms of X:
Y=X+Δ0
- Substitute Y into equation (2):
3X−2(X+Δ0)=0
Simplifying this gives:
3X−2X−2Δ0=0⟹X=2Δ0
- Substitute X back into the expression for Y:
Y=2Δ0+Δ0=3Δ0
5. Finding the Values of X and Y:
- Now, we can find the values of X and Y:
- From the equations, we have:
3X=2Y⟹3(−0.4Δ0)=2Y⟹Y=0.6Δ0
- Thus, we find:
X=−0.4Δ0(lowering of stabilized orbitals)
Y=0.6Δ0(raising of destabilized orbitals)
Conclusion:
- The lowering of the stabilized orbitals is 0.4Δ0 and the raising of the destabilized orbitals is 0.6Δ0.
- In a coordination compound, the five d-orbitals split into two sets due to the electrostatic interactions with surrounding ligands: the lower-energy set T2g (comprising dxy, dyz, and dzx) and the higher-energy set Eg (comprising dx2−y2 and dz2).
2. Defining Energies:
- Let X be the energy of stabilization for the T2g orbitals and Y be the energy of destabilization for the Eg orbitals.
- The total energy of separation due to the ligand field is denoted as Δ0.
- From the theory, we have the relationship:
Y−X=Δ0(1)
- The total stabilization energy for the T2g orbitals (3 orbitals) and destabilization for the Eg orbitals (2 orbitals) can be expressed as:
3X−2Y=0(2)
- From equation (1), we can express Y in terms of X:
Y=X+Δ0
- Substitute Y into equation (2):
3X−2(X+Δ0)=0
Simplifying this gives:
3X−2X−2Δ0=0⟹X=2Δ0
- Substitute X back into the expression for Y:
Y=2Δ0+Δ0=3Δ0
- Now, we can find the values of X and Y:
- From the equations, we have:
3X=2Y⟹3(−0.4Δ0)=2Y⟹Y=0.6Δ0
- Thus, we find:
X=−0.4Δ0(lowering of stabilized orbitals)
Y=0.6Δ0(raising of destabilized orbitals)
- The lowering of the stabilized orbitals is 0.4Δ0 and the raising of the destabilized orbitals is 0.6Δ0.
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Solved Examples
42 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Ex 7.1 Subjective (Terminology)
5 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Archives Subjective
23 Videos
- D AND F BLOCK ELEMENTSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - D AND F BLOCK ELEMENTSEXERCISE - Archives Subjective
29 Videos
Similar Questions
Knowledge Check
If the vertices of a triangle are (u,0),(v,8), and (0,0) then the area of the triiangle is
A4|u|B2|v|C|uv|D2|uv|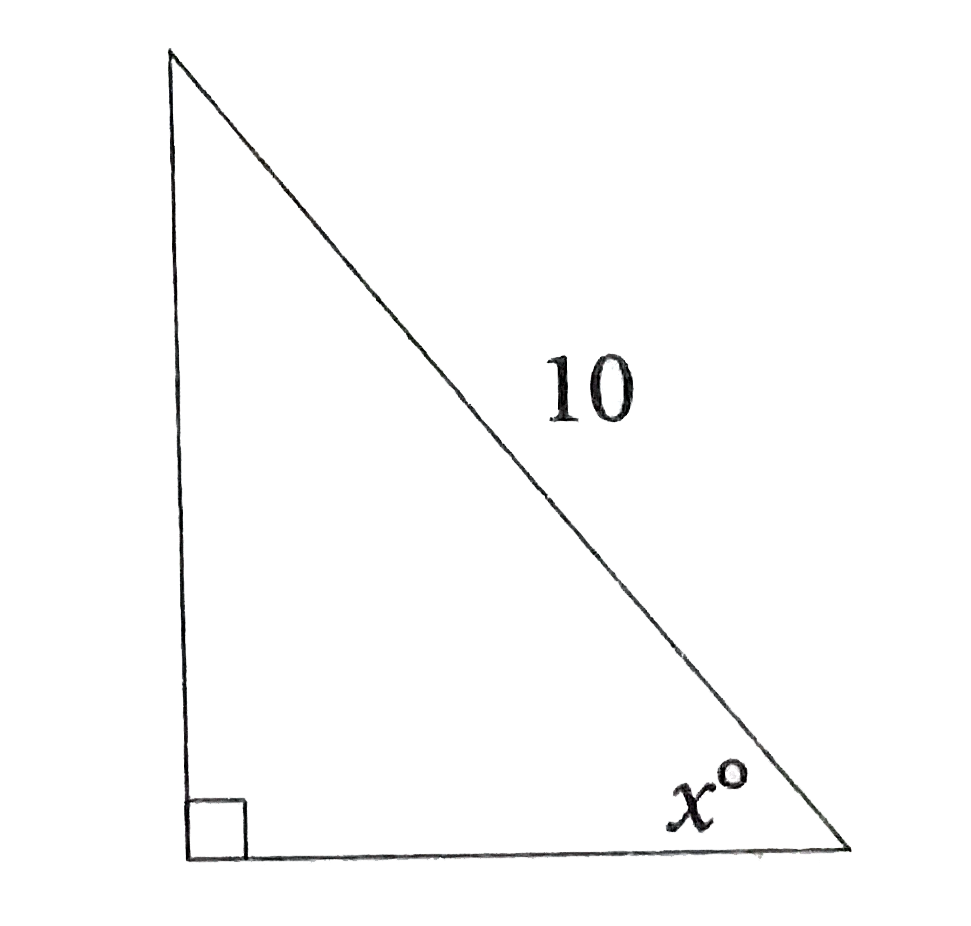
In the triangle above, sin x=0.8 and cos x=0.6. What is the area of the triangle?A0.48B4.8C24D48
Prove that measure of each of an equilateral triangle is 600
View SolutionProve that measure of each angle of an equilateral triangle is 600.
View SolutionProve that measure of each angle of an equilateral triangle is 600.
View SolutionConsider the following satements :
S1: Generally square planare complexes show geometrical isomerism but do not exhibit optical isomerism because thy do not possess plane of symmetry .
S2:Δt=49Δ0
S3: In octahedral complexes each electron entering teh t2g orbitals stabilizes the complex ion by 0.4 Δ0 and each electron entering teh eg orbital destabilizes the complex by an amount of 0.6 Δ0
Select the correct statement from the codes given below.
View SolutionΔE=0 for which process
View SolutionThe ends of the hypertenuse of right angled triangle are (0,6),(6,0) . The locus of the third vertex is
View Solution
