A point charge is placed at point A (1, 0, 2) m and another point charge is placed at point B (4, 4, 2) m. Find :
(i) Magnitude of electrostatic interaction force acting between them
(ii) Find (force on A due to B) and (force on due to A) in vector form
To solve the problem, we will follow these steps:
Given Data:
- Charge qA=+100μC=100×10−6C
- Charge qB=+200μC=200×10−6C
- Position of charge A: →A=(1,0,2)m
- Position of charge B: →B=(4,4,2)m
Step 1: Calculate the distance R between the charges
The distance R can be calculated using the distance formula in 3D:
R=√(x2−x1)2+(y2−y1)2+(z2−z1)2
Substituting the coordinates of A and B:
R=√(4−1)2+(4−0)2+(2−2)2
R=√(3)2+(4)2+(0)2=√9+16=√25=5m
Step 2: Calculate the electrostatic force F between the charges
Using Coulomb's Law:
F=k|qAqB|R2
Where k=14πϵ0≈9×109Nm2/C2.
Substituting the values:
F=9×109(100×10−6)(200×10−6)(5)2
F=9×109(100×200)×10−1225
F=9×10920000×10−1225
F=9×109×0.0008=7.2N
Step 3: Calculate the force vectors →FA and →FB
The force vector →FB on charge A due to charge B is given by:
→FB=F^r
Where ^r is the unit vector from A to B:
^r=→B−→AR=(4−1,4−0,2−2)5=(3,4,0)5=(35,45,0)
Thus,
→FB=7.2(35^i+45^j+0^k)
→FB=(7.2×35^i+7.2×45^j)=(4.32^i+5.76^j)N
For the force →FA on charge B due to charge A, it will be equal in magnitude but opposite in direction:
→FA=−→FB=−(4.32^i+5.76^j)=(−4.32^i−5.76^j)N
Final Answers:
1. The magnitude of the electrostatic interaction force F is 7.2N.
2. The force on A due to B →FA=(−4.32^i−5.76^j)N and the force on B due to A →FB=(4.32^i+5.76^j)N.
- Charge qA=+100μC=100×10−6C
- Charge qB=+200μC=200×10−6C
- Position of charge A: →A=(1,0,2)m
- Position of charge B: →B=(4,4,2)m
The distance R can be calculated using the distance formula in 3D:
R=√(x2−x1)2+(y2−y1)2+(z2−z1)2
Substituting the coordinates of A and B:
R=√(4−1)2+(4−0)2+(2−2)2
R=√(3)2+(4)2+(0)2=√9+16=√25=5m
Using Coulomb's Law:
F=k|qAqB|R2
Where k=14πϵ0≈9×109Nm2/C2.
F=9×109(100×10−6)(200×10−6)(5)2
F=9×109(100×200)×10−1225
F=9×10920000×10−1225
F=9×109×0.0008=7.2N
The force vector →FB on charge A due to charge B is given by:
→FB=F^r
Where ^r is the unit vector from A to B:
^r=→B−→AR=(4−1,4−0,2−2)5=(3,4,0)5=(35,45,0)
→FB=7.2(35^i+45^j+0^k)
→FB=(7.2×35^i+7.2×45^j)=(4.32^i+5.76^j)N
→FA=−→FB=−(4.32^i+5.76^j)=(−4.32^i−5.76^j)N
1. The magnitude of the electrostatic interaction force F is 7.2N.
2. The force on A due to B →FA=(−4.32^i−5.76^j)N and the force on B due to A →FB=(4.32^i+5.76^j)N.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems22videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)9videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
Similar Questions
A positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionFind out electric field intensity at point A (0, 1m, 2m) due to a point charge −20μC situated at point B(√2m,0,1m).
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View SolutionA point charge of 100μC is placed at 3ˆi+4ˆjm. Find the electric field intensity due to this charges at a point located at 9ˆi+12ˆjm.
View SolutionTwo point charges q1=20μC and q2=25μC are placed at (-1, 1, 1) m and (3, 1, -2)m, with respect to a coordinate system. Find the magnitude and unit vector along electrostatic force on q2 ?
View SolutionIn fig two equal positive point charge q1=q2=2.0μC. Interact with a third point charge Q=4.0μC. The magnitude as well as direction of the net force on Q is
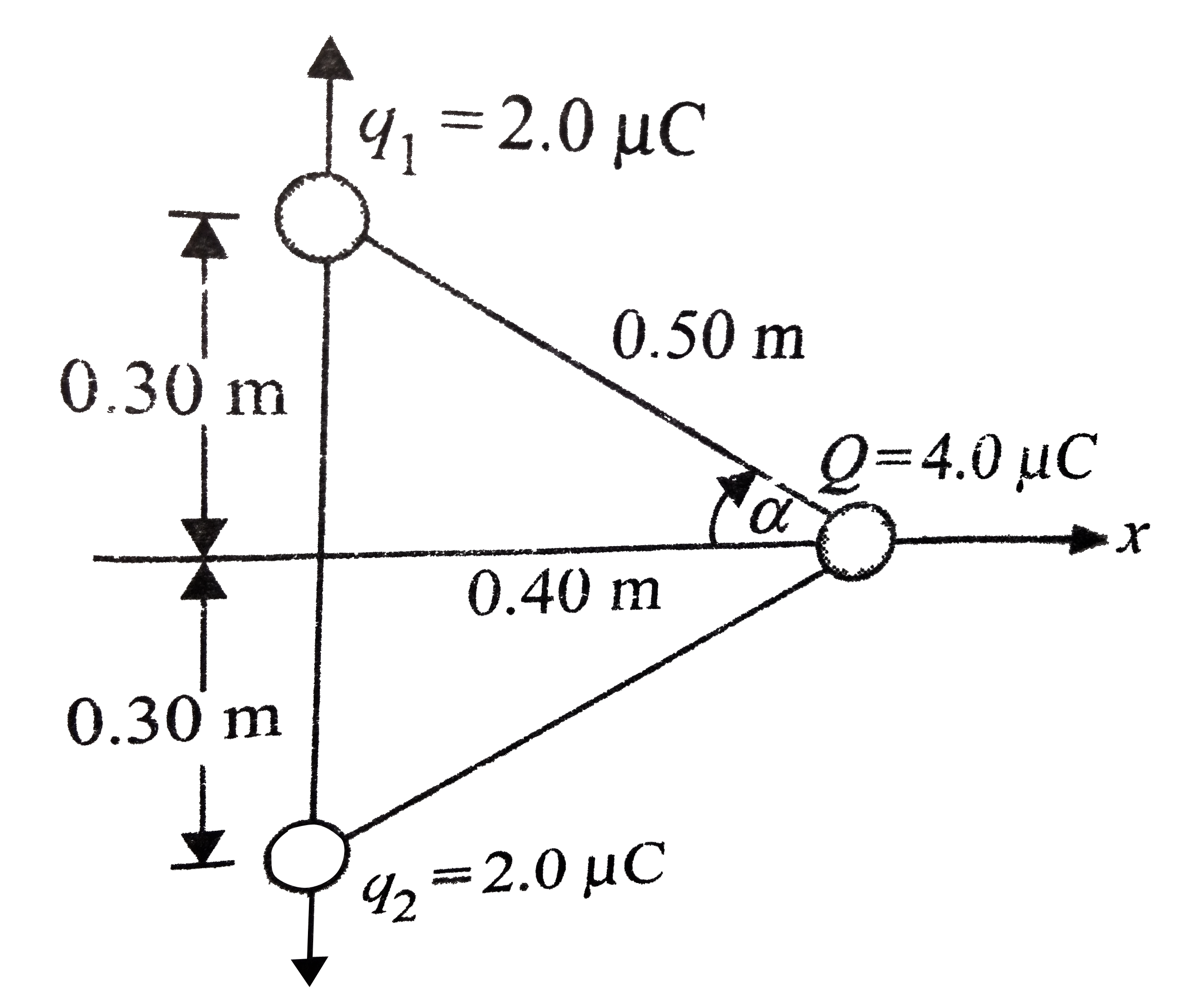 View Solution
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View SolutionAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:
 View Solution
View SolutionAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:
 View Solution
View SolutionA charge q1=2.00μC is located at the origin , and a charge q2=−6.00μC is located at (0,3.00)m.
(a) Find the total electric potential due to these charges at the point P hose coordinates are ( 4.00,0) m .
( b) Find the change in potential energy of the system of two charges plus a charge q3=3.00μC as the latter charge moves from infinity to point P .View Solution

