Photoelectric emission is observed from a surface for frequencies v1 and v2 of the incident radiation (v1>v2) if maximum kinetic energies of the photo electrons in the two cases are in the ratio 1:K, then the threshold frequency is given by :
v2−v1K−1
Kv1−v2K−1
Kv2−v1K−1
v2−v1K
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Photoelectric Effect
The photoelectric effect states that when light of a certain frequency strikes a material, it can eject electrons from that material. The kinetic energy (KE) of the emitted electrons can be expressed as:
KE=hν−ϕ
where:
- KE is the maximum kinetic energy of the emitted photoelectrons,
- h is Planck's constant,
- ν is the frequency of the incident radiation,
- ϕ is the work function of the material.
Step 2: Set Up the Equations for Two Frequencies
Given two frequencies ν1 and ν2 (where ν1>ν2), we can write the kinetic energies for these frequencies as:
KE1=hν1−ϕ
KE2=hν2−ϕ
Step 3: Use the Given Ratio of Kinetic Energies
According to the problem, the maximum kinetic energies are in the ratio 1:K:
KE1KE2=1K
Substituting the expressions for kinetic energy, we have:
hν1−ϕhν2−ϕ=1K
Step 4: Cross Multiply to Eliminate the Fraction
Cross multiplying gives us:
K(hν1−ϕ)=(hν2−ϕ)
Step 5: Rearrange the Equation
Expanding and rearranging the equation:
Khν1−Kϕ=hν2−ϕ
Khν1−hν2=Kϕ−ϕ
Khν1−hν2=ϕ(K−1)
Step 6: Solve for the Work Function ϕ
Now, we can solve for ϕ:
ϕ=Khν1−hν2K−1
Step 7: Relate Work Function to Threshold Frequency
The work function ϕ can also be expressed in terms of the threshold frequency ν0:
ϕ=hν0
Thus, we can set the two expressions for ϕ equal to each other:
hν0=Khν1−hν2K−1
Step 8: Solve for the Threshold Frequency ν0
Dividing both sides by h:
ν0=Kν1−ν2K−1
Final Result
The threshold frequency ν0 is given by:
ν0=Kν1−ν2K−1
The photoelectric effect states that when light of a certain frequency strikes a material, it can eject electrons from that material. The kinetic energy (KE) of the emitted electrons can be expressed as:
KE=hν−ϕ
where:
- KE is the maximum kinetic energy of the emitted photoelectrons,
- h is Planck's constant,
- ν is the frequency of the incident radiation,
- ϕ is the work function of the material.
Given two frequencies ν1 and ν2 (where ν1>ν2), we can write the kinetic energies for these frequencies as:
KE1=hν1−ϕ
KE2=hν2−ϕ
According to the problem, the maximum kinetic energies are in the ratio 1:K:
KE1KE2=1K
hν1−ϕhν2−ϕ=1K
Cross multiplying gives us:
K(hν1−ϕ)=(hν2−ϕ)
Expanding and rearranging the equation:
Khν1−Kϕ=hν2−ϕ
Khν1−hν2=Kϕ−ϕ
Khν1−hν2=ϕ(K−1)
Now, we can solve for ϕ:
ϕ=Khν1−hν2K−1
The work function ϕ can also be expressed in terms of the threshold frequency ν0:
ϕ=hν0
Thus, we can set the two expressions for ϕ equal to each other:
hν0=Khν1−hν2K−1
Dividing both sides by h:
ν0=Kν1−ν2K−1
The threshold frequency ν0 is given by:
ν0=Kν1−ν2K−1
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - ENABLE50videos
STRUCTURE OF ATOM
- BOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - EFFICIENT48videos
STRUCTURE OF ATOM
- BOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY-IIEXERCISE - JEE Advanced (Archive)43videos
STOICHIOMETRY-II
- BOOK - VMC MODULES ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - PRACTICE EXERCISE9videos
SURFACE CHEMISTRY
Similar Questions
Photoelectric emission is observed from a surface for frequencies v1andv2 of incident radiations
(v1>v2). If the maximum kinetic energy of photoelectrons in the two cases are in the ratio of 2:1 then threshold frequency v0 is given by.View SolutionPhotoelectric emission is observed from a metallic surface for frequencies v1 and v2 of the incident light rays (v1>v2). If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio of 1:k , then the threshold frequency of the metallic surface is
View Solution
Knowledge Check
- Question 1 - Select One
The photoeletric threshold 4v is incident on the metal is v. When light of freqency 4v is incident on the metal, the maximum kinetic energy of the emitted photoelectron is
A4hvB3hvC5hvD5hv2
Photoelectric emission is observed from a metallic surface for frequencies v1 and v2 of the incident light rays (v1>v2). If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio of 1:k , then the threshold frequency of the metallic surface is
View SolutionPhotoelectric emmision is observed from a surface when lights of frequency n1and n2 incident.If the ratio of maximum kinetic energy in two cases is K:1 then ( Assume n1>n2) threshod frequency is
View SolutionThe photoelectric threshold frequency of a metal is v. When light of frequency 4v is incident on the metal . The maximum kinetic energy of the emitted photoelectrons is
View SolutionMaximum kinetic energy (Ek) of a photoelectron varies with the frequency (v) of the incident radiation as
View SolutionA If the wavelength of the incident radiation changes from λ1 to λ2 then the maximum kinetic energy of the emitted photo electrons changes from K to K,, then the work function of the emitter surface is
View SolutionGiven in fig. is the graph between frequency v of the incident light and maximum kinetic energy (Ek) of the emitted photoelectrons. Find the values of (i) threshold frequency and (ii) work function form the graph.
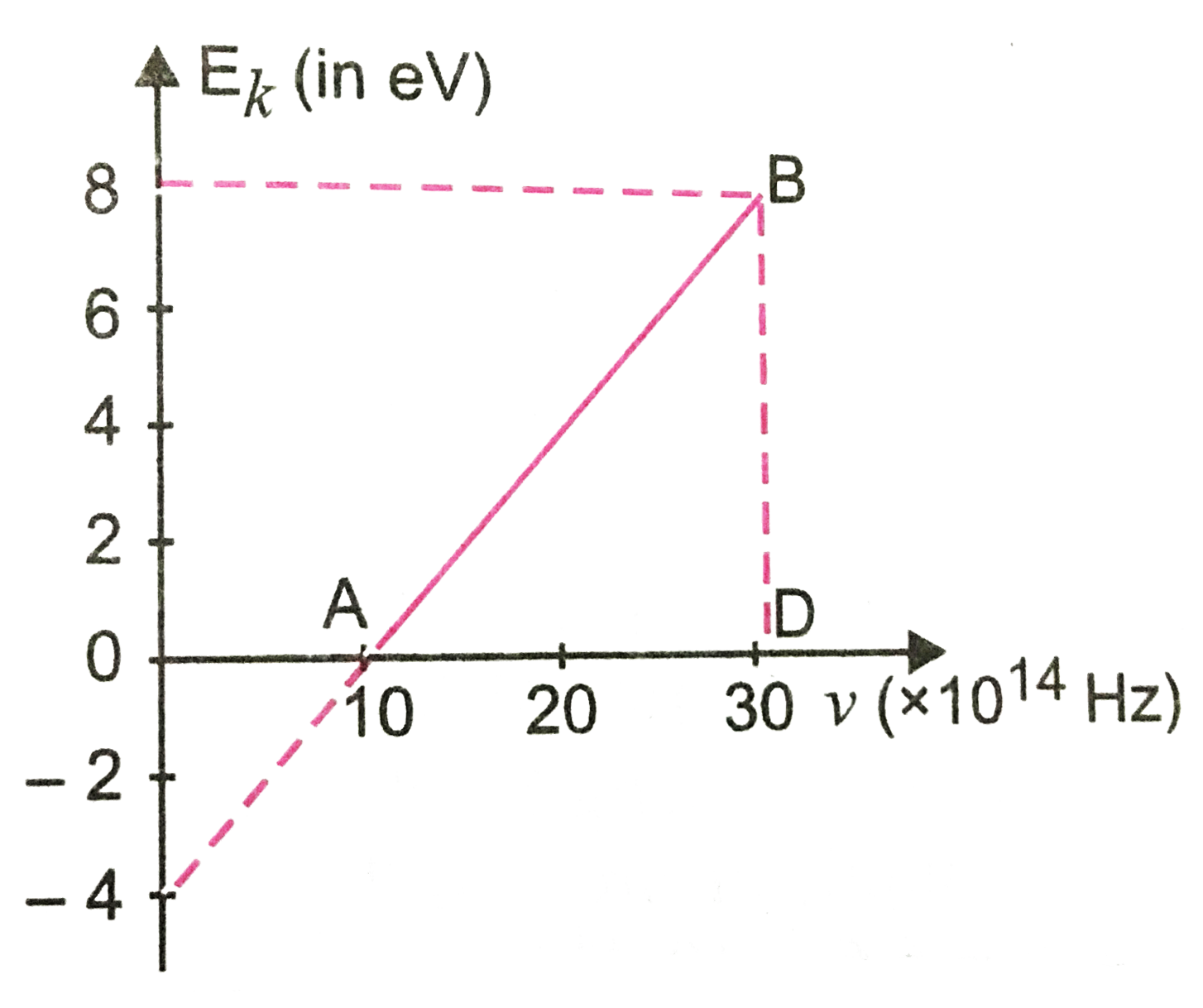 View Solution
View SolutionThe work functions of metals A and B are in the ratio 1:2. If light of frequencies f and 2f are incident on the surfaces of A and B respectively , the ratio of the maximum kinetic energy of photoelectrons emitted is ( f is greater than threshold frequency of A,2f is greater than threshold frequency of B)
View Solution

