If b,k are intercepts of a focal chord of the parabola y 2 =4ax then k is equal to
A
b+c2
B
bcb+c
C
2bcb+c
D
√bc
Text Solution
The correct Answer is:C
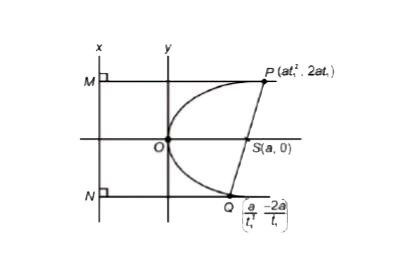
Let P(at21,2at1)andQ(at22,2at2) are end points of a chord
PQ is a focal chord
t1t2=−1
t2=−1t1
Q(at21,−2at1)
b=SP=PM=a+at21
b−a=at21...........(i)
c=SQ=QN=a+at21
c−a=at21...........(ii)
|
Similar Questions
Knowledge Check
If b,c are the segments of a focal chord of the parabola y2=4ax, then c is equal to
Aabb−aBbb−cCab−aDaba−bIf b and k are segments of a focal chord of the parabola y2=4ax, then k =
Aabb−aBbb−aCab−aDaba−bThe locus of the poles of focal chords of the parabola y2=4ax is
Ax=0Bx=−aCx=2aDy=0
If t is the parameter for one end of a focal chord of the parabola y2=4ax, then its length is :
View SolutionIf t is the parameter for one end of a focal chord of the parabola y2=4ax, then its length is :
View SolutionIf t is the parameter for one end of a focal chord of the parabola y2=4ax, then its length is :
View SolutionIf tangents at extremities of a focal chord AB of the parabola y2=4ax intersect at a point C, then ∠ACB is equal to
View SolutionIf tangents at extremities of a focal chord AB of the parabola y2=4ax intersect at a point C, then ∠ACB is equal to
View Solution
