Find the number of roots of equation xsinx=1Solution in Tamil
To find the number of roots of the equation ex=√−x ,we draw the graphs of y=exandy=√−x and check the number of points of intersection.
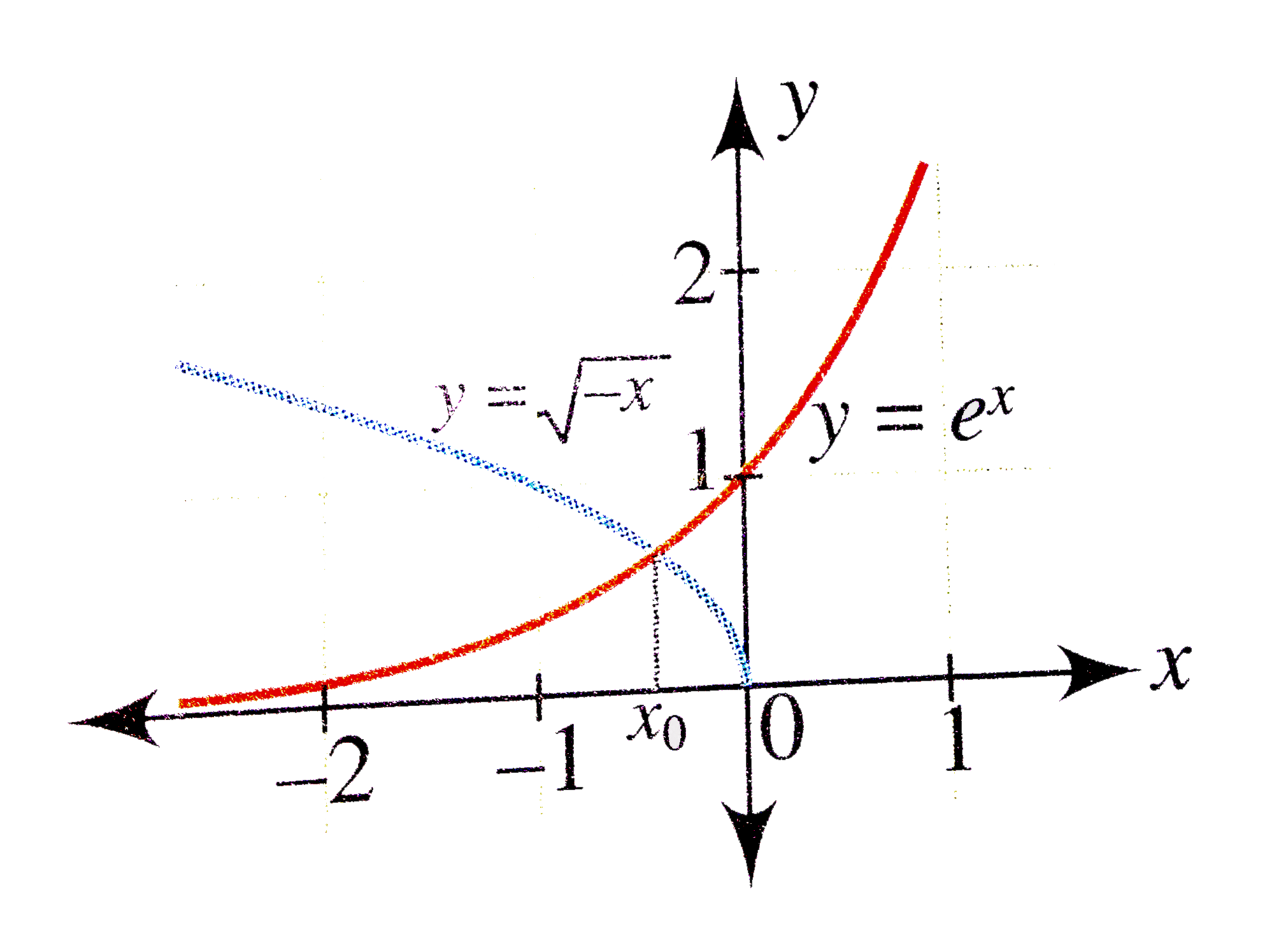
From the figure, there is only one point of intersection, hence only one root x0.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
04:56View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=007:52View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
00:45View SolutionFind the number of roots of equation xsinx=1
03:52View SolutionWhich of the following is/are correct?
(A) Between any two roots of excosx=1, there exists at least one root of tanx=1.
(B) Between any two roots of exsinx=1, there exists at least one root of tanx=−1.
(C) Between any two roots of excosx=1, there exists at least one root of exsinx=1.
(D) Between any two roots of exsinx=1, there exists at least one root of excosx=1.04:53View SolutionFind the number of roots of the equation xlogex=1.
02:21View Solutionअवकल समीकरण xcosxdydx+y(xsinx+cosx)=1 का हल ज्ञात कीजिये।
05:31View SolutionFind the number of roots of equation xsinx=1
01:28View SolutionThe number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π] is (a) 2 (b) 3 (c) 4 (d) 0
02:45View SolutionWhich of the following is/are correct?
(A) Between any two roots of excosx=1, there exists at least one root of tanx=1.
(B) Between any two roots of exsinx=1, there exists at least one root of tanx=−1.
(C) Between any two roots of excosx=1, there exists at least one root of exsinx=1.
(D) Between any two roots of exsinx=1, there exists at least one root of excosx=1.04:35View SolutionFind the number of roots of the equation xlogex=1.
03:56View SolutionFind the number of roots of equation xsinx=1
04:23View SolutionBetween any two real roots of the equation exsinx−1=0, the equation excosx+1=0 has :
10:10View SolutionFind the number of roots of equation xsinx=1
04:45View SolutionThe number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π] is 2 (b) 3 (c) 4 (d) 0
10:02View SolutionWhich of the following is/are correct? (A) Between any two roots of e^xcosx=1, there exists at least one root of tanx=1. (B) Between any two roots of e^xsinx=1, there exists at least one root of tanx=-1. (C) Between any two roots of e^xcosx=1, there exists at least one root of e^xsinx=1. (D) Between any two roots of e^xsinx=1, there exists at least one root of e^xcosx=1.
02:18View Solution

