D,E,F are three points on the sides BC,CA,AB, respectively, such that ∠ADB=∠BEC=∠CFA=θ. A′,B'C' are the points of intersections of the lines AD,BE,CF inside the triangle. Show that are of A′B′C′=4cos2θ, where is the area of ABC.Solution in Tamil
From ΔAB'CAB'sin(π−(A+θ))=ACsin(π−B)

⇒AB'=2Rsin(A+θ)
From ΔAC'B,AC'sin(θ−A)=ABsin(π−C)
⇒AC'=2Rsin(θ−A)
∴B'C'=2R(sin(A+θ)−sin(θ−A))
=4RcosθsinA=2acosθ
Similarly, C'A'=2bcosθ
∴ Area of ΔA'B'C'=12(B'C')(A'C')sin∠B'C'A'
=12(2acosθ)(2bcosθ)sinC
=4cos2θ×Δ
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.112videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.28videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank15videos
PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCE
Similar Questions
Find the value of a2+b2+c2R2 in any right-angled triangle.
01:35View SolutionIf the sides of a triangle are a, b and √a2+ab+b2, then find the greatest angle
04:23View SolutionIt is given that in a group of 4 students, the probability of 2 students not having the same birthday is 0.893. What is the probability that the 2 students have the same birthday?
02:10View SolutionThe area of a right triangle is 6864 sq. units. If the ratio of its legs is 143:24, then the value of r is ______
03:25View SolutionIf f(x)<0, x∈(a,b) then at the point C(c, f(c)) on y=f(x) for whichF(c) is a maximum, f′(c) is given by a.f′(c)=f(b)−f(a)b−1 b. f′(c)=f(b)−f(a)a−b c.f′(c)=2(f(b)−f(a))b−a d. f′(c)=0
02:07View SolutionD, E and F are the points on sides BC, CA and AB respectively of ABC such that AD bisects ∠A, BE bisects ∠B and CF bisects ∠C . If AB=5cm, BC=8cm and CA=4cm , determine AF, CE and BD .
05:38View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
03:43View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
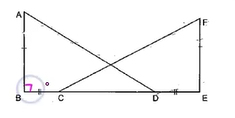
04:18View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
 03:49View Solution
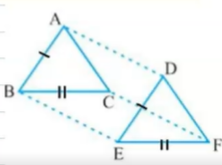
03:49View SolutionIf ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
 02:07View Solution
02:07View SolutionIf D,EandF are three points on the sides BC,CAandAB, respectively, of a triangle ABC show that the BDCD=CEAE=AFBF=−1
03:31View SolutionThe sides BC,CA and AB of a triangle ABC, are produced in order, forming exterior angles ∠ACD,∠BAE and ∠CBF . Show that ∠ACD+∠BAE+∠CBF=3600
07:07View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC . Prove that DF⋅EF=FB⋅FA.
02:06View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DE∣∣BC.
04:00View SolutionO is any point inside a triangle ABC . The bisector of ∠AOB,∠BOC and ∠COA meet the sides AB,BC and CA in point D,EandF respectively. Show that AD⋅BE⋅CF=DB⋅EC⋅FA
04:58View SolutionD, E and F are the points on sides BC, CA and AB respectively of ABC such that AD bisects ∠A, BE bisects ∠B and CF bisects ∠C . If AB=5cm, BC=8cm and CA=4cm , determine AF, CE and BD .
03:05View Solution

