The region represented by the inequality |2z-3i|<|3z-2i| is
A
the unit disc with its centre at z=0
B
the exterior of the unit circle with its centre at z=0
C
the inerior of a square of side 2 units with its centre at z=0
D
none of these
Text Solution
The correct Answer is:B
(b) |2z−3i|2<|3z−2i|2
∴4x2+(2y−3)2<9x2+(3y−2)2
∴x2+y2>1
∴|z|2>1
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The shaded region is represented by the inequality:
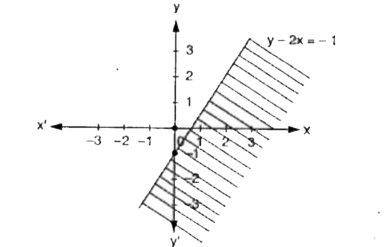 Ay−2x≤−1Bx−2y≤−1Cy−2x≥−1Dx−2y≥−1
Ay−2x≤−1Bx−2y≤−1Cy−2x≥−1Dx−2y≥−1 - Question 2 - Select One
The region represented by the inequations 2x+3y≤18,x+y≥10,x≥0,y≤0 is
Aa polygonBunboundedCbondedDnull region - Question 3 - Select One
The shaded region is represented by the inequation:
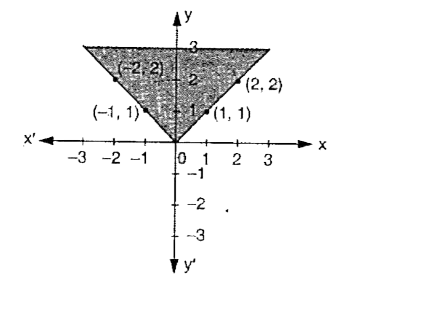 Ay≥xBy≥−xCy≥|x|Dy≤|x|
Ay≥xBy≥−xCy≥|x|Dy≤|x|
Construct the region represented by the inequations x+y≤3andx−y≤2.
View SolutionConstruct the region represented by the inequations 2x+y≤2andx−3y≤3
View SolutionConstruct the region represented by the inequations x+y≥4and3x+2y≤6.
View SolutionConstruct the region represented by the inequation x+3y≥3and3x+y≤3
View SolutionShade the region represented by the inequations. x+y≤3 and 3x−2y≥4.
View Solution

