Let and are complex numbers such that . If and are the roots of the , then which one of the following is correct ?Solution in Tamil
and
and
If , then and vice versa
Nothing definite can be said
The correct Answer is:A
and
Given
……….
but ……..
From and
{ must be positive}
If
.........
Also
..........
From and
and
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Complex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
03:16View Solutionz1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
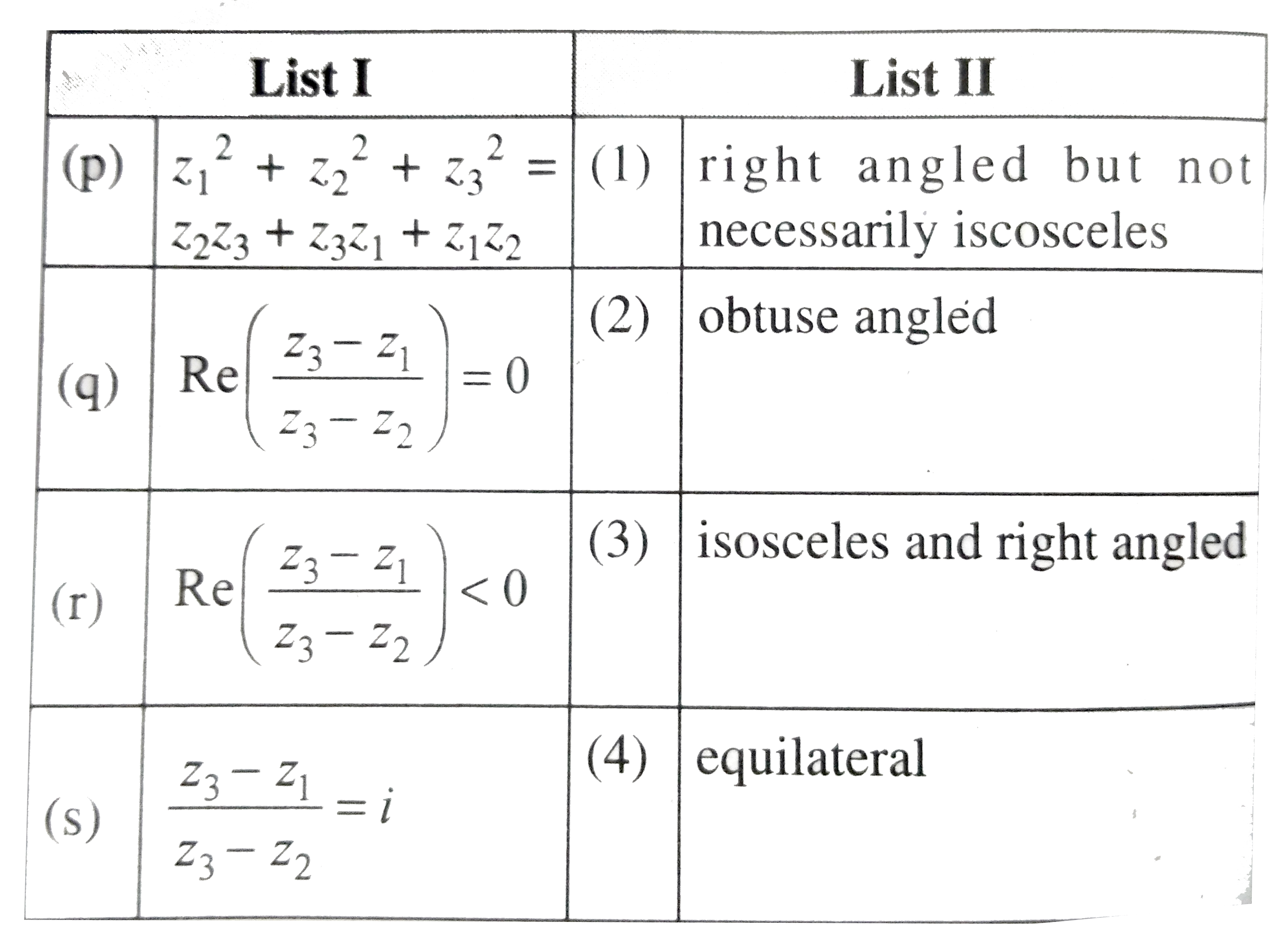
Codes08:43View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
05:21View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
05:34View SolutionZ_(1) and Z_(2) are two complex numbers represented by the plans A and B in the argand Plane Z,AndZ_(2) are the roots of Z^(2)+pZ+q=0./_AOB=alpha alpha!=0 and 0 is origin and OA= OB,then (p^(2))/(q) is equal to
07:20View SolutionIf from a point P representing the complex number z_(1) on the curve |z|=2, two tangents are drawn from P to the curve |z|=1 , meeting at points Q(z_(2)) and R(z_(3)), then :
03:22View SolutionLet p and q are complex numbers such that |p|+|q|<1. If z1 and z2 are the roots of the z2+pz+q=0, then which one of the following is correct ?
05:31View SolutionP(z1),Q(z2),R(z3)andS(z4) are four complex numbers representing the vertices of a rhombus taken in order on the comple plane, then which one of the following is/are correct?
06:50View SolutionIf P andn Q are represented by the complex numbers z1 and z2 such that |1/z2+1/z1|=|1/z2−1/z1|, then
04:17View SolutionThe points P,Q denote the complex numbers, ¯z1,¯z2 in the Argand diagram. O. is the origin. If ¯¯¯¯¯¯¯z1z2+¯¯¯¯¯¯¯z2z1=0, show that ∠POQ=90∘
03:46View SolutionIf P(z1),Q(z2),R(z3) and S(z4) are four complex numbers representing the vertices of a rhombus taken in order on the complex plane, which one of the following is held good?
06:39View Solutionz1 व z2 समीकरण z2+pz+q=0 के मूल हैं जहाँ गुणांक p व q सम्मिश्र संख्याएँ हो सकती हैं। A तथा B सम्मिश्र तल में z1 व z2 को प्रदर्शित करते हैं। यदि ∠AOB=a≠0 तथा OA=OB जहाँ O मूलबिन्दु है, तब कौन-सा कथन सत्य है?
04:20View SolutionLet A and B represent z1 and z2 in the Argand plane and z1,z2 be the roots of the equation Z2+pZ+q=0 ,where p,q are complex numbers. If O is the origin, OA=OB and ∠AOB=α then p2=
03:20View SolutionLet z1 and z2 be the roots of the equation z2+pz+q=0, where p,q are real. The points represented by z1,z2 and the origin form an equilateral triangle if
02:24View SolutionLet p and q are complex numbers such that |p|+|q|<1. If z1 and z2 are the roots of the z2+pz+q=0, then which one of the following is correct ?
07:39View SolutionIf P and Q are represented by the complex numbers z1 and z2 such that ∣∣∣1z2+1z1∣∣∣=∣∣∣1z2−1z1∣∣∣, then
03:21View Solution

