If the tangents at z1, z2 on the circle |z−z0|=r intersect at z3, then (z3−z1)(z0−z2)(z0−z1)(z3−z2) equals
A
1
B
−1
C
i
D
−i
Text Solution
The correct Answer is:B
(b) 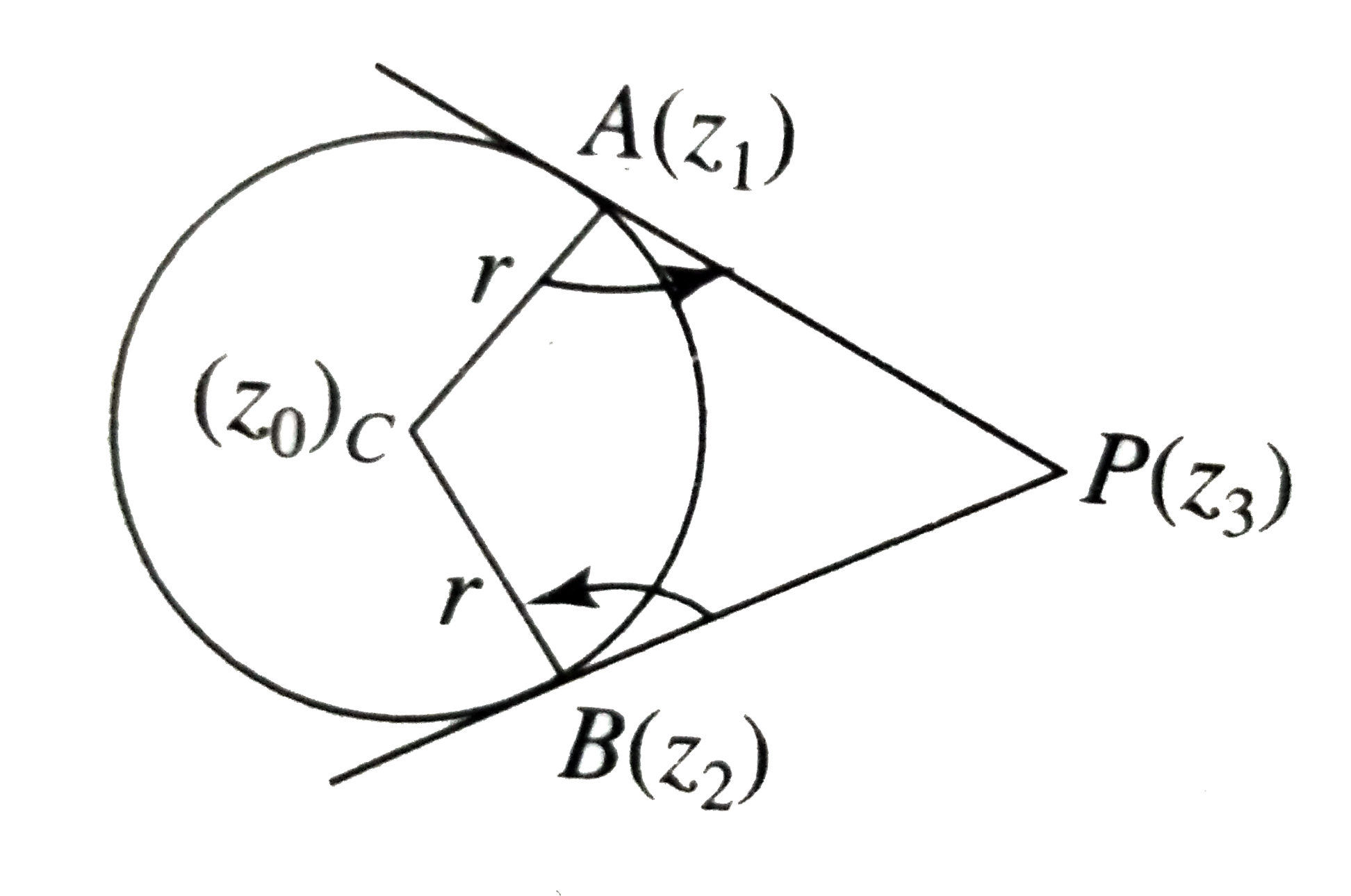
z3−z1z0−z1=(PAAC)i and z0−z2z3−z2=(BCBP)i
∴(z3−z1)(z0−z2)(z0−z1)(z3−z2)=(PAAC×BCPB)(−1)=−1
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The tangents at z1,z2 on the circle |z−z0|=a, meet at z3. Then (z3−z1z0−z1)(z0−z2z3−z2) is equal to
A0B1C−1D2 - Question 2 - Select One
If tangent at Z1,Z2 on the circle |Z−Z0|=r intersect at Z3. Then(Z3−Z1)(Z0−Z2)(Z0−Z1)(Z3−Z2) equals.
A1B−1C0Dnone of the above
If z1,z2andz3 are the vertices of an equilateral triangle, then 1z1−z2+1z2−z3+1z3−z1=0
View SolutionGiven z1+3z2−4z3=0 then z1,z2,z3 are
View SolutionIf z1,z2,z3 are three distinct non-zero complex numbers and a,b,c∈R+ such that a|z1−z2|=b|z2−z3|=c|z3−z1|,thena2z1−z2+b2z2−z3+c2z3−z1isequa<o Re(z1+z2+z3) (b) Img(z1+z2+z3) 0 (d) None of these
View SolutionIf z1,z2,z3 are complex numbers such that |z1|=|z2|=|z3|=∣∣∣1z1+1z2+1z3∣∣∣=1 then |z1+z2+z3| is equal to
View SolutionThe centre of a square ABCD is at z0. If A is z1 , then the centroid of the ABC is 2z0−(z1−z0) (b) (z0+i(z1−z03) z0+iz13 (d) 23(z1−z0)
View SolutionLet z1z2,z3, be three complex number such that z1+z2+z3=0 and |z1|=|z2|=|z3|=1 then Let ∣∣z21+2z22+z23∣∣ equals
View Solution

