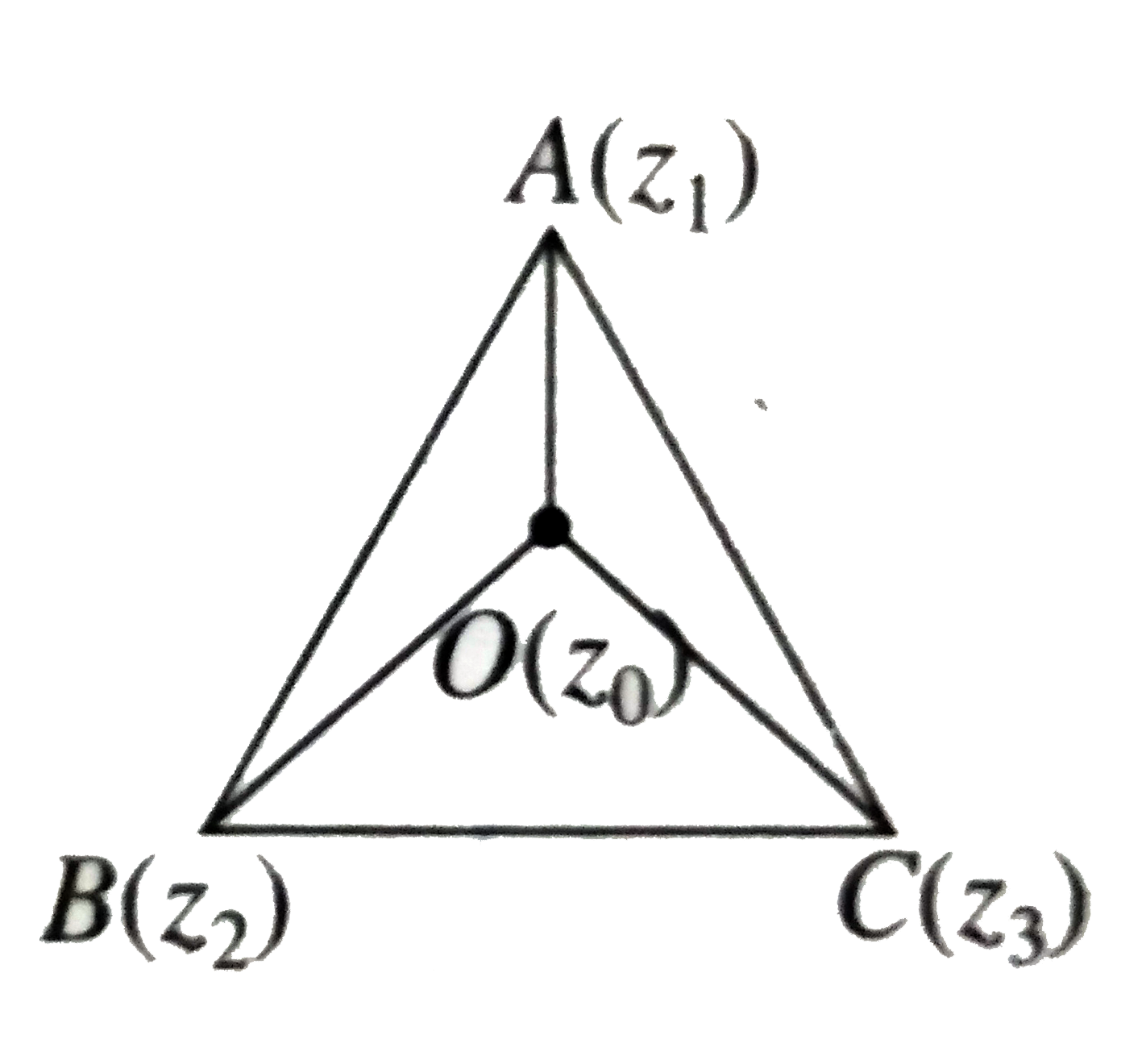
If $z_{1}$ , $z_{2}$ and $z_{3}$ are the vertices of $Δ A B C$ , which is not right angled triangle taken in anti-clock wise direction and $z_{0}$ is the circumcentre, then $(\frac{z_{0} - z_{1}}{z_{0} - z_{2}}) \frac{sin 2 A}{sin 2 B} + (\frac{z_{0} - z_{3}}{z_{0} - z_{2}}) \frac{sin 2 C}{sin 2 B}$ is equal to

A

$0$

B

$1$

C

$- 1$

D

$2$

Text Solution

Verified by Experts

The correct Answer is:C

$(c)$ Takin rotation at $' O'$ ltbr> $\frac{z_{0} - z_{1}}{z_{0} - z_{2}} = cos 2 C - i sin 2 C$
$\frac{z_{0} - z_{3}}{z_{0} - z_{2}} = cos 2 A + i sin 2 A$
Now $(\frac{z_{0} - z_{1}}{z_{0} - z_{2}}) \frac{sin 2 A}{sin 2 B} + (\frac{z_{0} - z_{3}}{z_{0} - z_{2}}) \frac{sin 2 C}{sin 2 B}$
$= sin 2 A cos 2 C - i sin 2 A sin 2 C$
$= \frac{+ cos 2 A sin 2 C + i sin 2 A sin 2 C}{sin 2 B}$
$= \frac{sin (2 A + 2 C)}{sin 2 B} = - 1$

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $z_{1}, z_{2} and z_{3}$ be the vertices of $Δ A B C$ , taken in anti-clock wise direction and $z_{0}$ be the circumstance, then $(\frac{z_{0} - z_{1}}{z_{0} - z_{2}}) \frac{sin 2 A}{sin 2 B} + (\frac{z_{0} - z_{3}}{z_{0} - z_{2}}) \frac{sin 2 C}{sin 2 B}$ is equal to
A0
B1
C $- 1$
D2
Question 2 - Select One
If $z_{1}, z_{2}, z_{3}$ are the vertices of an isoscles triangle right angled at $z_{2}$ , then
A $z_{1}^{2} + 2 z_{2}^{2} + z_{3}^{2} = 2 z_{2} (z_{1} + z_{3})$
B $z_{1}^{2} + z_{2}^{2} + z_{3}^{2} = 2 z_{2} (z_{1} + z_{3})$
C $z_{1}^{2} + z_{2}^{2} + 2 z_{3}^{2} = 2 z_{2} (z_{1} + z_{3})$
D $2 z_{1}^{2} + z_{2}^{2} + z_{3}^{2} = 2 z_{2} (z_{1} + z_{3})$
Question 3 - Select One
The tangents at $z_{1}, z_{2}$ on the circle $| z - z_{0} | = a$ , meet at $z_{3}$ . Then $(\frac{z_{3} - z_{1}}{z_{0} - z_{1}}) (\frac{z_{0} - z_{2}}{z_{3} - z_{2}})$ is equal to
A $0$
B $1$
C $- 1$
D $2$

CENGAGE-COMPLEX NUMBERS-JEE Advanced Previous Year

Home
Ask Doubt
Profile