Let f(x)=sgn(cot−1x)+tan(π2[x]), where [x] is the greatest integer function less than or equal to x, then which of the following alternatives is/are true? f(x) is many-one but not an even function. f(x) is a periodic function. f(x) is a bounded function. The graph of f(x) remains above the x-axis.Solution in Tamil
f(x) is many-one but not an even function.
f(x) is a periodic function.
f(x) is a bounded function.
The graph of f(x) remains above the x-axis.
The correct Answer is:A, B, C, D
f(x)=sgn(cot−1x)+tan(π2[x])
sgn(cot−1x) is dedfined when cot−1x is defined, which is ∀x∈R.
tan(π2[x]) is defined when π2[x]≠(2n+1)2π, where n∈Z,
or[x]≠2n+1orx∈[2n+1,2n+2).
Hence, domain of f(x) is ∪n∈Z[2n,2n+1).
Also, cot−1x>0∀x∈R. Then
f(x)=1+tan(π2[x])=1
∴f(x)=1,x∈Df

From the graph, f(x) si periodic with period 2.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)32videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)9videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Single)125videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank28videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Consider the functions
f(x)={x+1,x≤12x+1,1<x≤2andg(x)={x2,−1≤x<2x+2,2≤x≤3
The domain of the function f(g(x)) is02:02View SolutionThe function f(x) is defined on the interval [0, 1]. Now, match the following lists:
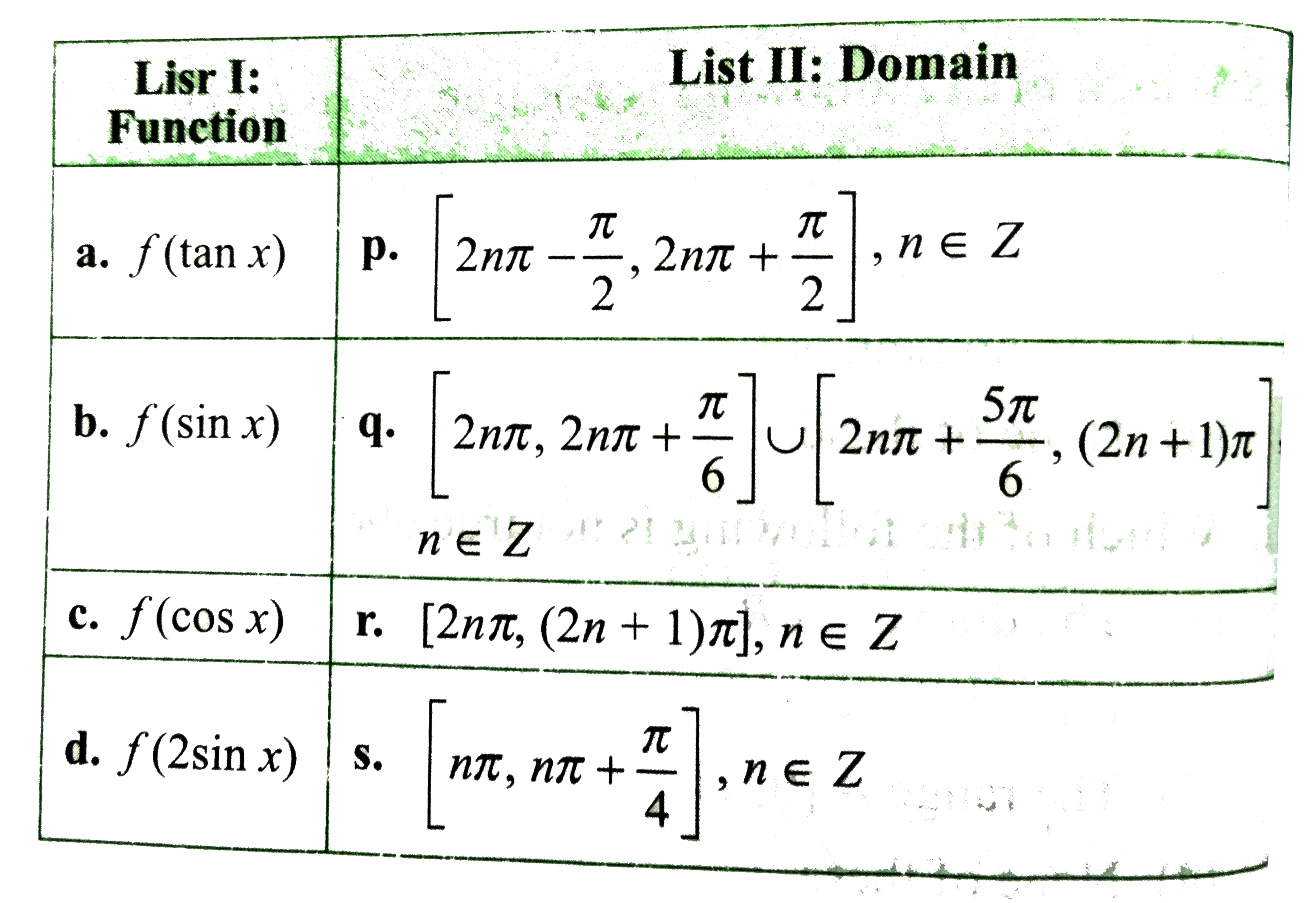 07:18View Solution
07:18View SolutionThe relation R={(1,1),(2,2),(3,3),(1,2),(2,3),(1,3)} on a set A={1, 2, 3} is
03:21View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
04:13View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
03:15View SolutionLet f(x)=cos(pi(|x|+2[x])) where [.] represents greatest integer function,then then (1) f(x) is neither odd nor even (2)f(x) is non periodic function ( 3 ) Range of f(x) is [-1,1] (4) f(x)=|f(x)| for all x .
05:05View SolutionLet f(x)=sgn(cot−1x)+tan(π2[x]), where [x] is the greatest integer function less than or equal to x, then which of the following alternatives is/are true? f(x) is many-one but not an even function. f(x) is a periodic function. f(x) is a bounded function. The graph of f(x) remains above the x-axis.
03:57View SolutionIn which of the following function, range is not singleton set f(x)=[x]+[−x] (b) f(x)={x}+{−x} f(x)=|sgn(x)| (d) f(x)=[√x−[x] where [x],{x},andsgn(x) are greatest integer function, fractional part function and signum function respectively.
02:09View SolutionLet f (x)= tan/x, then the value of lim_(x->oo) ([f(x)]+x^2)^(1/({f(x)})) is equal to (where [.] , {.} denotes greatest integer function and fractional part functions respectively) -
View SolutionIf the function f:R rarr R be such that f(x)=x-[x], where [x] denotes the greatest integer less than or equal to x, then f^(-1)(x) is
03:20View SolutionThe function f(x)=sgn(x−1).Cot−1[x−1] is ([x]denotes greatest integer function of x)
02:39View SolutionIf F(x)=sinπ[x]{x} then F(x) is (where {.} denotes fractional part function and [.] denotes greatest integer function and sgn(x) is a signum function)
02:06View SolutionThe function f(x)=tan|π[x−π]|1+[x]2, where [x] denotes the greatest integer less than or equal to x, is
04:47View SolutionLet f(x)=exsgn(x+[x]) , where sgn is the signum function and [x] is the greatest integer function . Then
07:01View SolutionLet f(x)=sgn(cot−1x)+tan(π2[x]), where [x] is the greatest integer function less than or equal to x, then which of the following alternatives is/are true? f(x) is many-one but not an even function. f(x) is a periodic function. f(x) is a bounded function. The graph of f(x) remains above the x-axis.
04:27View SolutionThe function f(x)=tan|π[x−π]|1+[x]2, where [x] denotes the greatest integer less than or equal to x, is
08:18View Solution

