Find the maximum value of f(x)=(1x)xSolution in Tamil
We have f(x)=(1x)x
Clearly, domain of the function is x>0
Differentiating we get, f′(x)=(1x)x(log1x−1)
f′(x)=0⇒log1x=1=logee⇒1x=e⇒x=1e
Also for x<1/e,f′(x) is positive and for x>1/e,f′(x) is negative.
Therefore, the maximum value of the function is e1/e.
Also, limx→0(1x)x=elimx→0xlog(1x)=e-limx→0xlogx=e−x→0limlogx1x=e−x→0lim1x−1x2=e0=1
limx→∞(1x)x=0
From the above discussion, the graph of the function is as shown in the following figure.
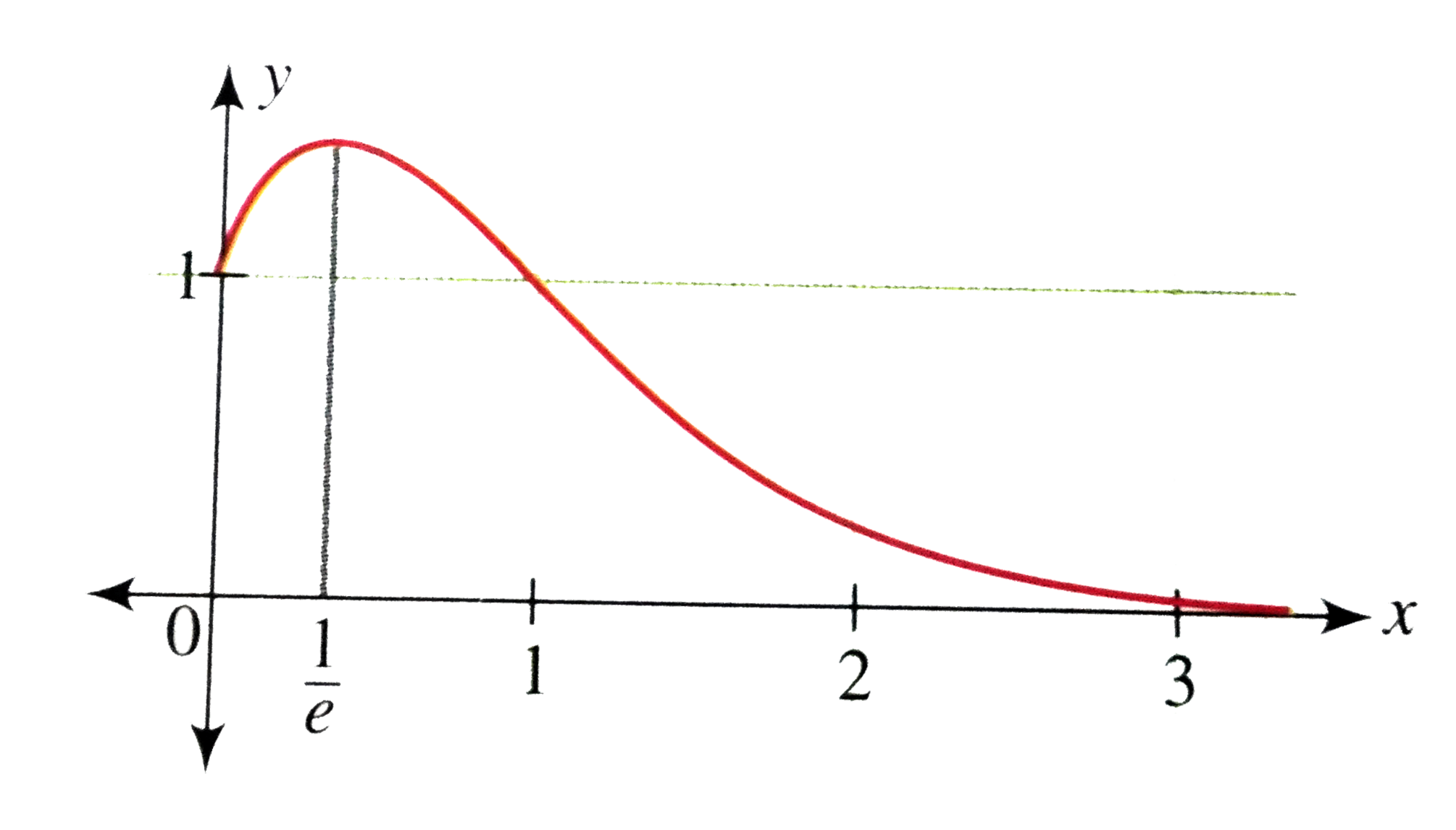
Topper's Solved these Questions
Similar Questions
Draw the graph of y=sin2x−cosx
05:11View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
01:16View SolutionSolve: (x+2)3=2x(x2−1)
01:25View SolutionIf f(x)=|x-1|+|x-2|-|x-3|, then (a) maximum value of f(x) is 3 if x in[2,3] (b) maximum value of f(x) is -3 if x in[1,3] (c) maximum value of f(x) is -3 if x in[1,2] (d) maximum value of f(x) is 3 if x in[1,3]
04:47View SolutionFind the maximum value of f(x)=x2+x+1 in [0,1] .
02:01View Solutionif f(x)=(x^(3))/(3)-x^(2)+(1)/(5) find maximum and minimum value of f(x)
02:48View SolutionFind maximum and minimum values , if any , of the function f given by f(x) = x4+1,x∈R.
04:01View SolutionFind the maximum and minimum value of f if any of the function f(x)=|x−1|,x∈R .
05:42View Solutionf(x)=5−|x−1|. Find the maximum value of f(x), also find the value of x for which f(x) is maximum.
02:36View SolutionIf f(x)=|x−2|+x2−1andg(x)+f(x)=x2+3, find the maximum value ofg(x).
02:06View SolutionIf the maximum and minimum value of f(x)=a+b sin x be 7 and 1 respectively, find the values of f(π6).
02:48View SolutionThe maximum value of
f(x) , if f(x) + f(1x)=1x,x∈ domain of f05:59View SolutionFind the maximum and minimum values of f(x)=(1−x)+|x|
02:35View SolutionFind the absolute maximum and absolute minimum values of f on the given interval f(x)=xx+1 [1 , 2]
02:11View SolutionThe maximum value of f(x)=(1x)x is …………
02:54View Solutionमाना f(x)=x−1x है। x∈(0,4) के लिए f(x) के अधिकतम तथा न्यूनतम मान ज्ञात कीजिये।
02:54View Solution

