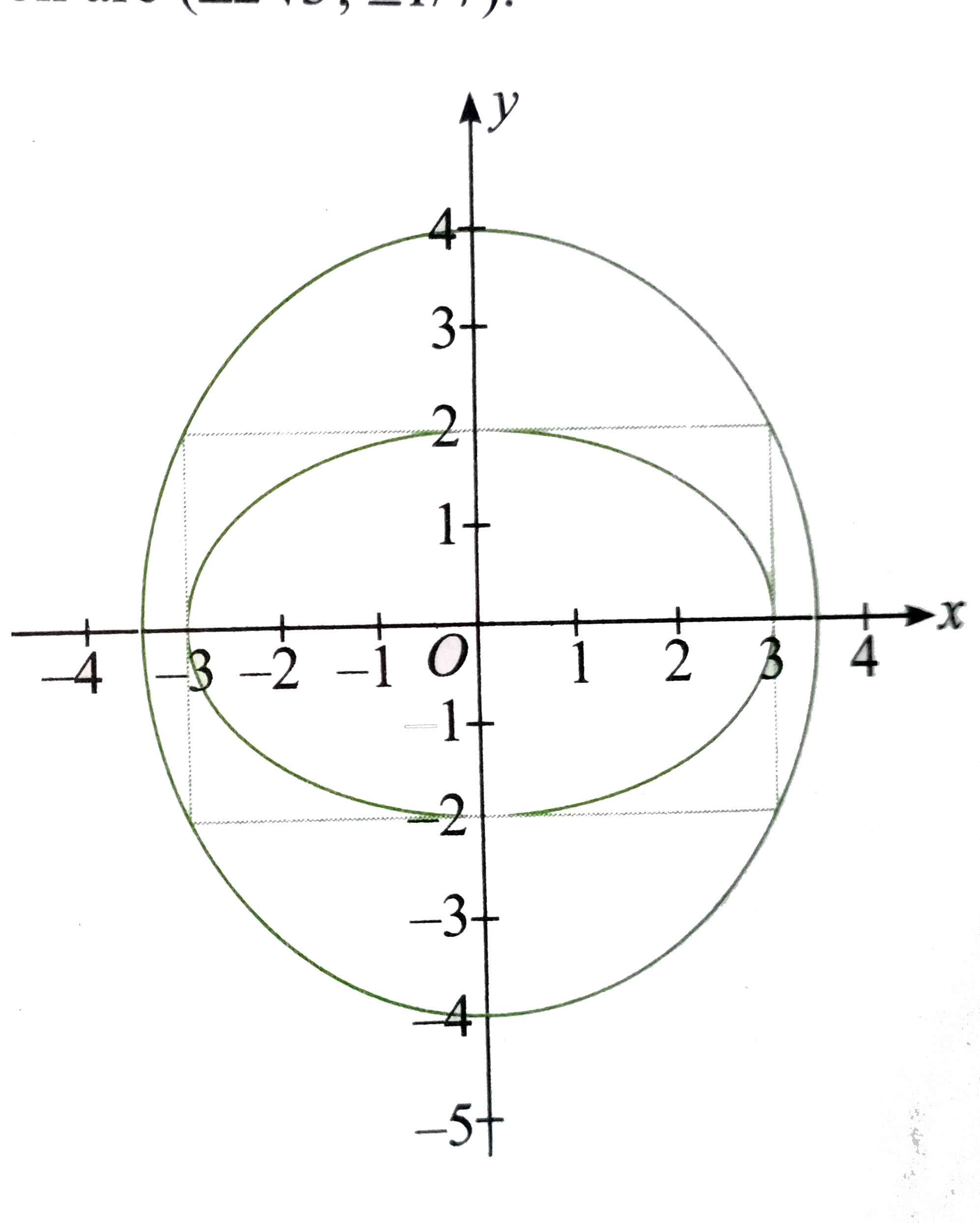
The ellipse E1:(x^2)/9+(y^2)/4=1 is inscribed in a rectangle R whose s

The ellipse $x^{2} + 4 y^{2} = 4$ is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is (1) $x^{2} + 16 y^{2} = 16$ (2) $x^{2} + 12 y^{2} = 16$ (3) $4 x^{2} + 48 y^{2} = 48$ (4) $4 x^{2} + 64 y^{2} = 48$
A $x^{2} + 12 y^{2} = 16$
B $4 x^{2} + 48 y^{2} = 48$
C $4 x^{2} + 64 y^{2} = 48$
D $x^{2} + 16 y = 16$
The ellipse $x^{2} + 4 y^{2} = 4$ is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is (1) $x^{2} + 16 y^{2} = 16$ (2) $x^{2} + 12 y^{2} = 16$ (3) $4 x^{2} + 48 y^{2} = 48$ (4) $4 x^{2} + 64 y^{2} = 48$
A $x^{2} + 16 y^{2} = 16$
B $x^{2} + 12 y^{2} = 16$
C $4 x^{2} + 48 y^{2} = 16$
D $4 x^{2} + 64 y^{2} = 48$
Ellipse $x^{2} + 4 y^{2} = 4$ is inscribed in a rectangle aligned with co-ordinate axes . This rectangle itself is inscribed in another ellipse the passes ellipse that through (-4,0) . Then the equation of the ellipse is
A $x^{2} + 16 y^{2} = 16$
B $x^{2} + 12 y^{2} = 16$
C $4 x^{2} + 48 y^{2} = 48$
D $4 x^{2} + 64 y^{2} = 48$

Let the ellipse be
$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
as it passing through (0,4) and (3,2). So,
$b^{2} = 16 and \frac{9}{a^{2}} + (4) + (16) = 1$
or $a^{2} = 12$ ltbr So, $12 = 16 (1 - e^{2})$
or $e = \frac{1}{2}$