Using the relation or otherwise, prove that
Give that
To prove sin , let us consider
f(x)=sin(tanx )-x
f(x) =cos (tanx )
Therefore .Thus f(x) is an increasing function
so ,for x in we have
or
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Illustration2videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise 6.110videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank13videos
METHODS OF DIFFERETIATION
- BOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Using constraint method find the relation between accelerations of 1 and 2.
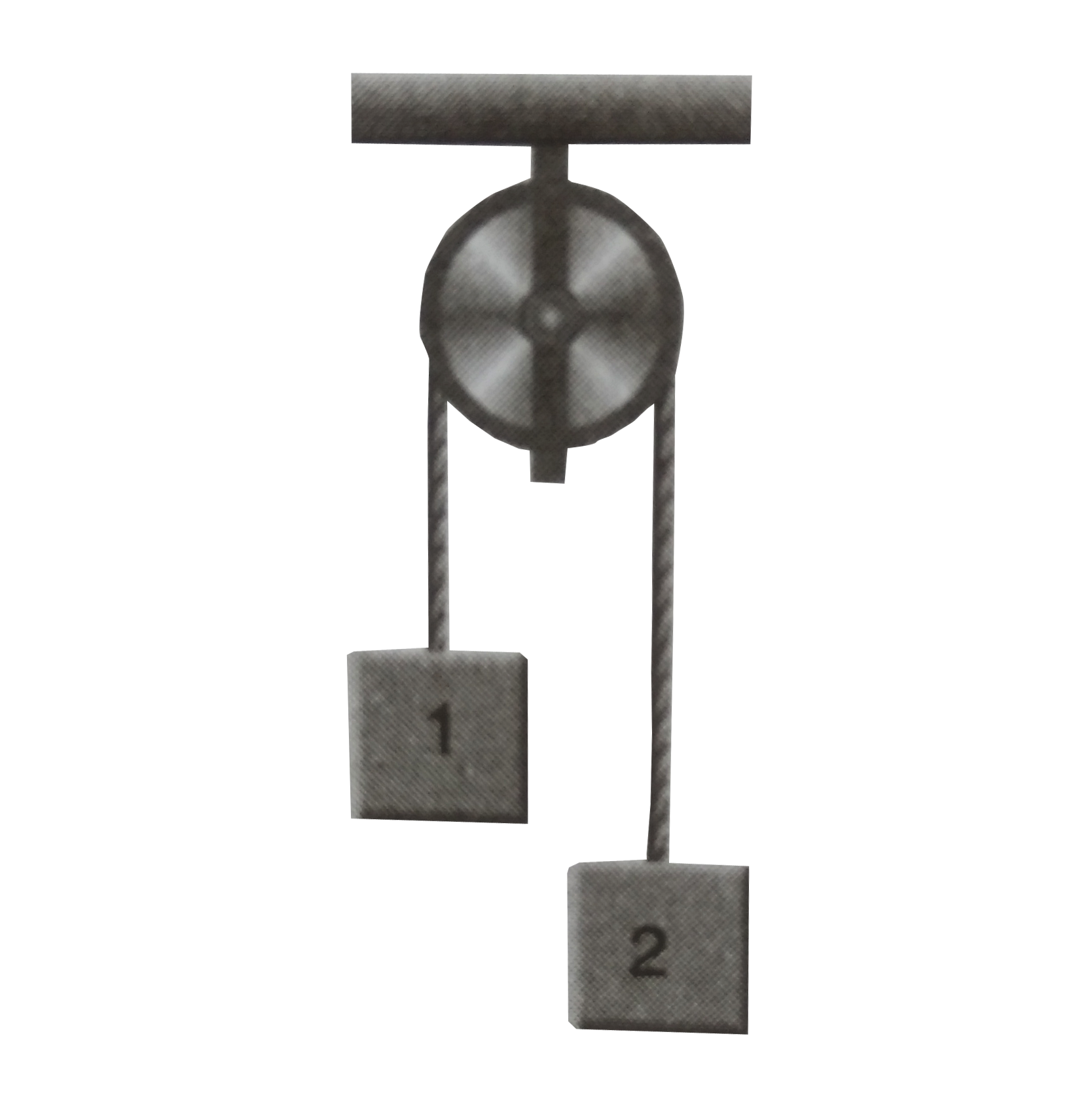
 View Solution
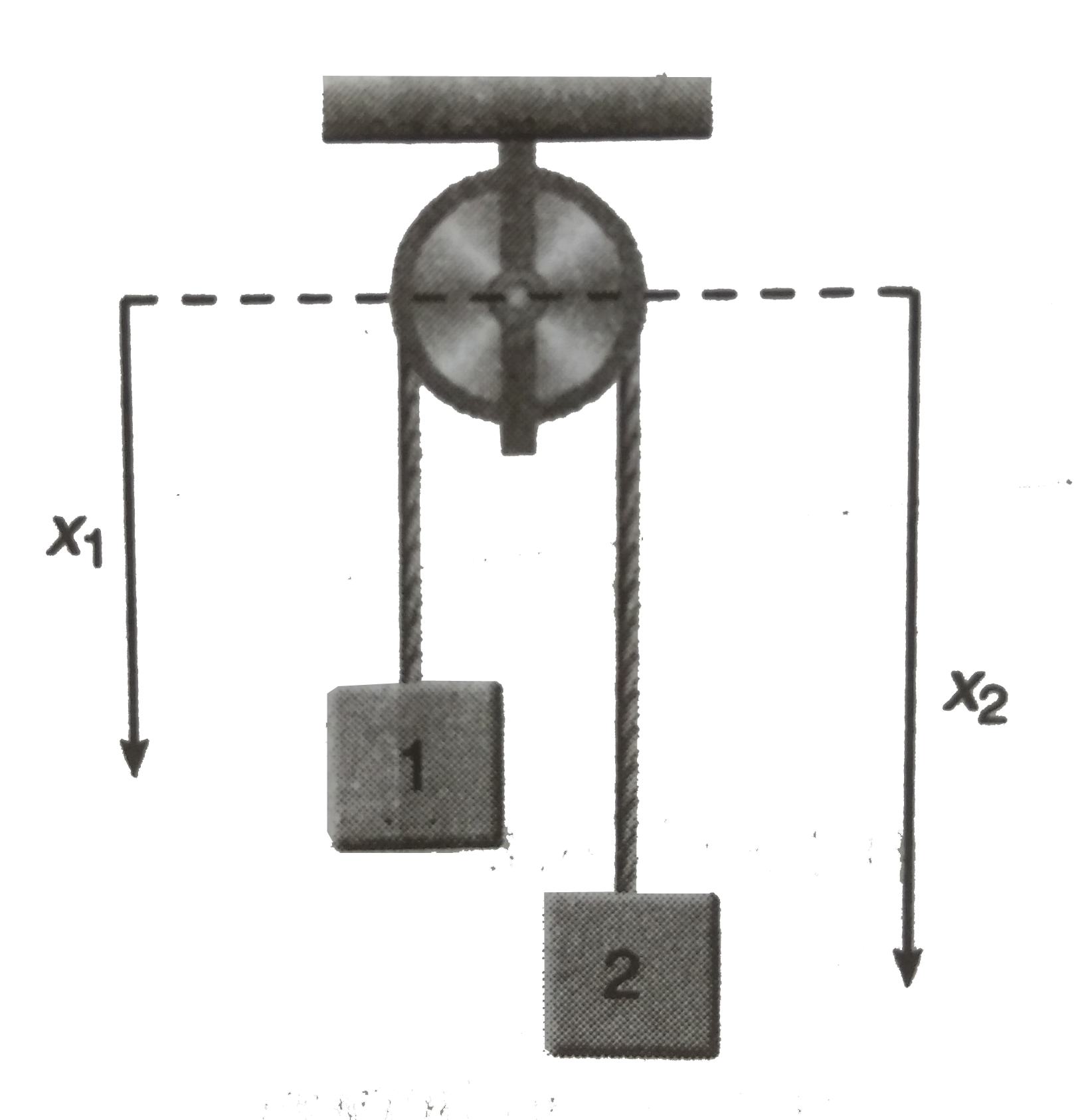
View SolutionUsing constraint method find the relation between accelerations of 1 and 2.
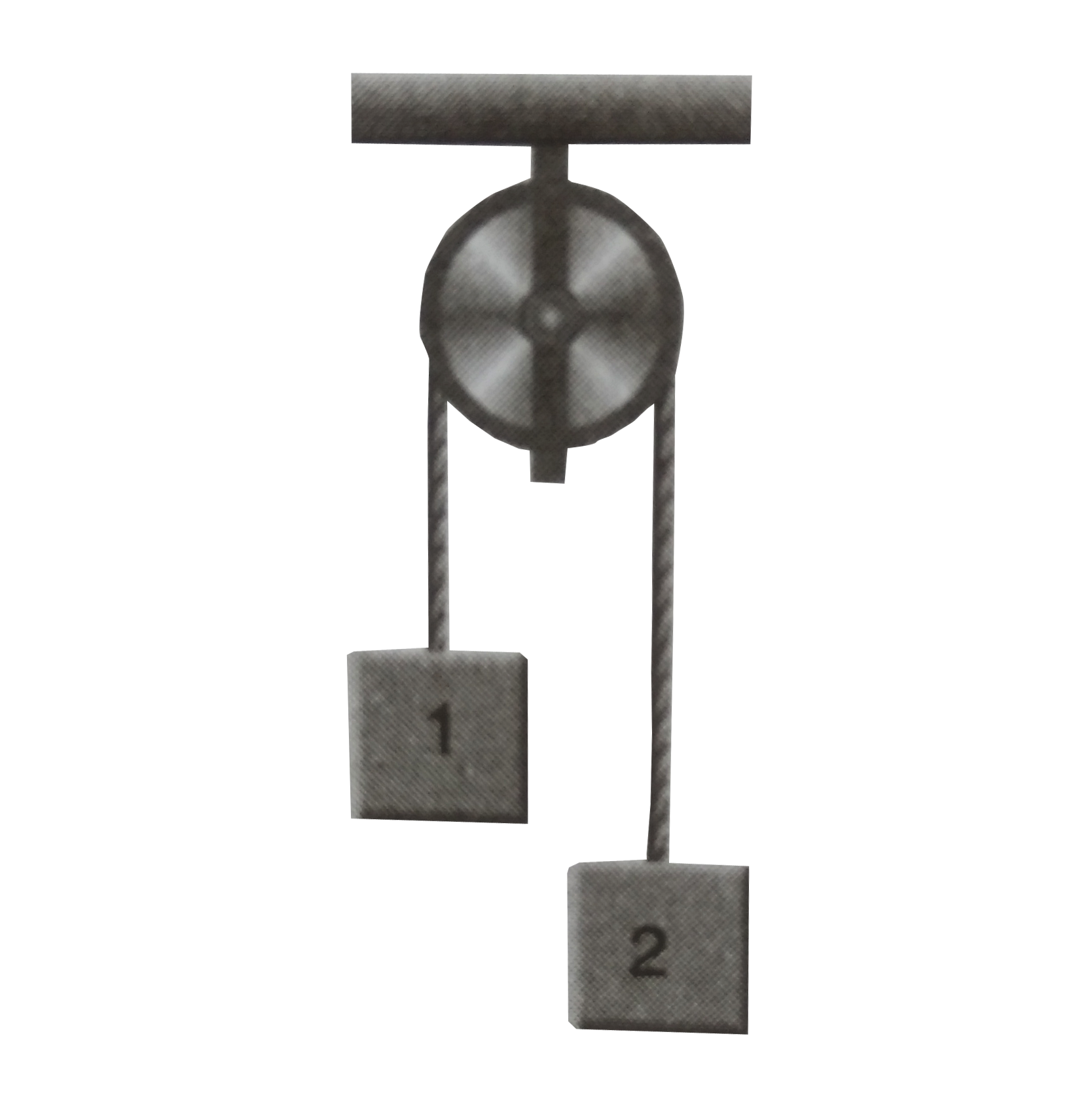
 View Solution
View SolutionUsing constraint method find the relation between of a1 and a2.
 View Solution
View SolutionUsing constraint method find the relation between of a1 and a2.
 View Solution
View SolutionFind the differentiation of y=tan−1 ⎷1+cosx21−cosx2
View SolutionUsing contraint equation. Find the relation between a1anda2.
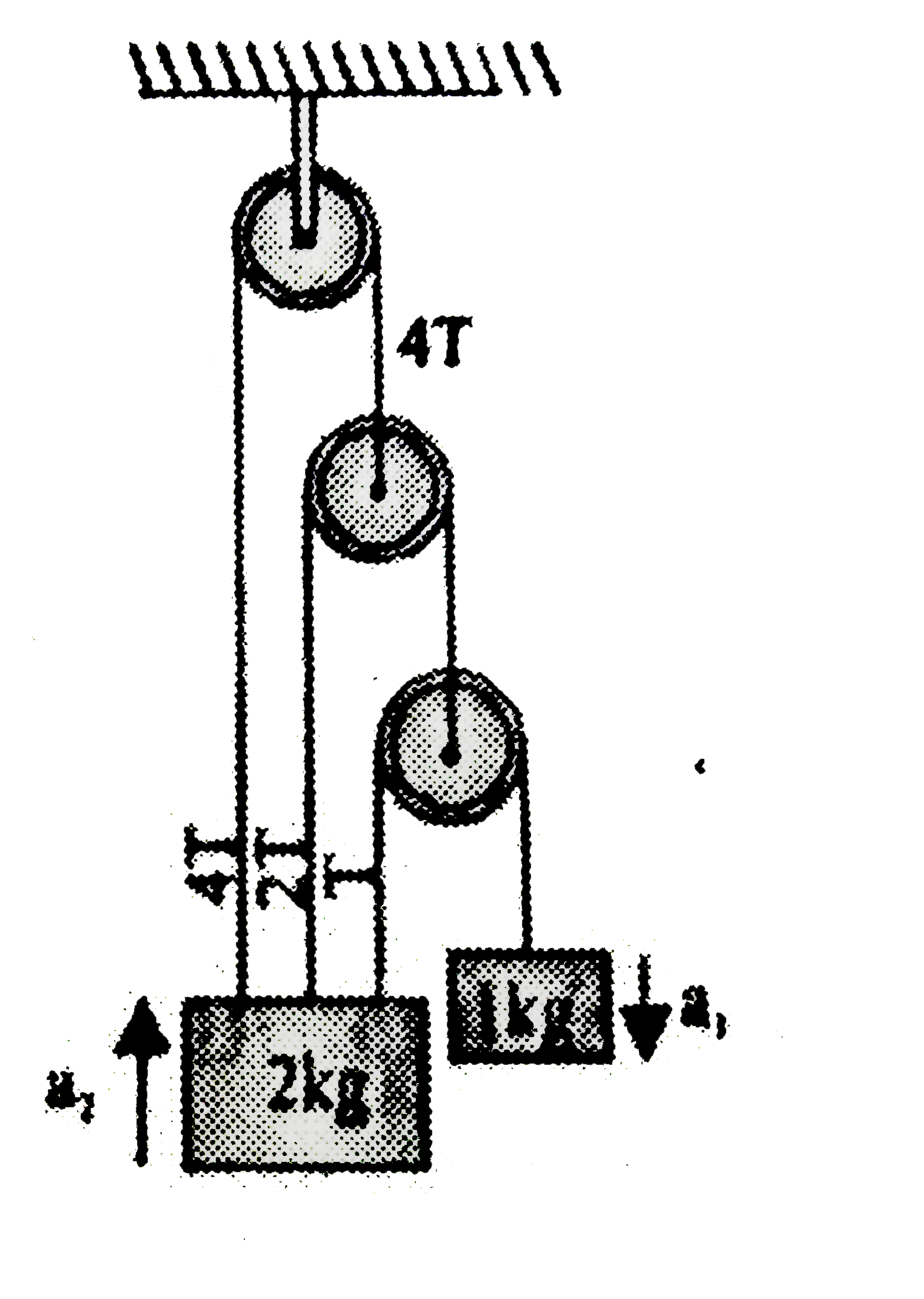 View Solution
View SolutionUsing contraint equation. Find the relation between a1anda2.
 View Solution
View SolutionProve that
1+sinx−cosx1+sinx+cosx+1+sinx+cosx1+sinx−cosx
=2 cosec xView SolutionProve that
1+sinx−cosx1+sinx+cosx+1+sinx+cosx1+sinx−cosx
=2 cosec xView SolutionIf f(x) =∣∣ ∣∣sinxcosxsinxcosx−sinxcosxx11∣∣ ∣∣ find the value of 2(f'(o))+{f'(1)}2
View Solution

