Resistance in the two gaps of a meter bridge are 10ohm and 30ohm respectively. If the resistances are interchanged he balance point shifts by
The correct Answer is:6ms−1
To solve the problem step by step, we will analyze the situation using the principles of a meter bridge.
Step 1: Understand the setup
We have a meter bridge with two resistances in its gaps: R1=10Ω and R2=30Ω. The balance point is determined by the ratio of the resistances.
Step 2: Calculate the balance point for the first arrangement
Using the formula for the balance point in a meter bridge:
R1R2=L1100−L1
Substituting the values of R1 and R2:
1030=L1100−L1
This simplifies to:
13=L1100−L1
Step 3: Cross-multiply to find L1
Cross-multiplying gives:
L1=13(100−L1)
Expanding this:
3L1=100−L1
Rearranging gives:
3L1+L1=100
4L1=100
L1=25cm
Step 4: Calculate the balance point for the second arrangement
Now, we interchange the resistances, so R1=30Ω and R2=10Ω. Again, we use the balance point formula:
R1R2=L2100−L2
Substituting the new values:
3010=L2100−L2
This simplifies to:
3=L2100−L2
Step 5: Cross-multiply to find L2
Cross-multiplying gives:
3(100−L2)=L2
Expanding this:
300−3L2=L2
Rearranging gives:
300=4L2
L2=75cm
Step 6: Calculate the shift in the balance point
The shift in the balance point when the resistances are interchanged is given by:
Shift=L2−L1
Substituting the values:
Shift=75cm−25cm=50cm
Final Answer
The balance point shifts by 50 cm.
---
We have a meter bridge with two resistances in its gaps: R1=10Ω and R2=30Ω. The balance point is determined by the ratio of the resistances.
Using the formula for the balance point in a meter bridge:
R1R2=L1100−L1
Substituting the values of R1 and R2:
1030=L1100−L1
This simplifies to:
13=L1100−L1
Cross-multiplying gives:
L1=13(100−L1)
Expanding this:
3L1=100−L1
Rearranging gives:
3L1+L1=100
4L1=100
L1=25cm
Now, we interchange the resistances, so R1=30Ω and R2=10Ω. Again, we use the balance point formula:
R1R2=L2100−L2
Substituting the new values:
3010=L2100−L2
This simplifies to:
3=L2100−L2
Cross-multiplying gives:
3(100−L2)=L2
Expanding this:
300−3L2=L2
Rearranging gives:
300=4L2
L2=75cm
The shift in the balance point when the resistances are interchanged is given by:
Shift=L2−L1
Substituting the values:
Shift=75cm−25cm=50cm
The balance point shifts by 50 cm.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV B14videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-V A20videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III26videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
Similar Questions
The resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is
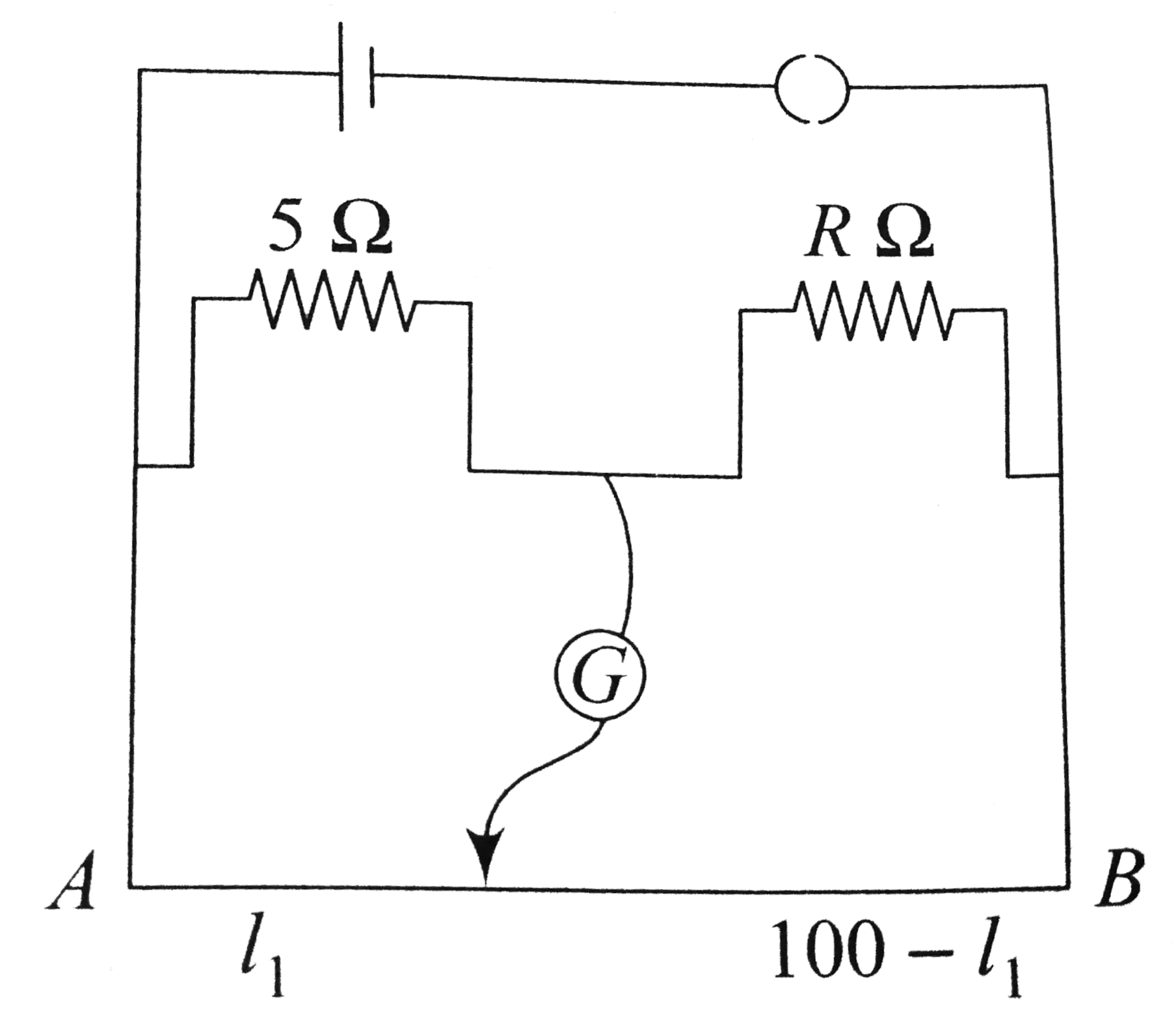 View Solution
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm
A resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm) and an unknown resistance, greater than 2Ωis conneted across the other gap. When these resistances are interchanged, the balance point shifts by 20cm. Neglecting any corrections,the unknown resistance is
View SolutionA resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm and an unknown resistance, greater than 2Ω, is connected across the other gap. When these resistance are interchanged, the balance point shifts by 20cm. Neglecting any corrections, the unknown resistance is.
(a)3Ω
(b) 4Ω
( c) 5Ω
(d) 6Ω.View SolutionThe resistance of the four arms P,Q,R and S in a Wheatstone's bridge are 10ohm30ohm and 90ohm rerspectively. The e.m.f. and internal resistance of the cell are 7V and 5ohm respectively. If the galvanometer resistance is 50ohm, the current drawn for the cell will be
View SolutionThe resistance in two arms of the meter bridge is 10Ω and x respectively. The balance length is l1from left. Now the resistance of 10Ω is shunted with another resistor of resistance equal to unknown resistance x then new balance point is 0.75l1 The value of resistance x is
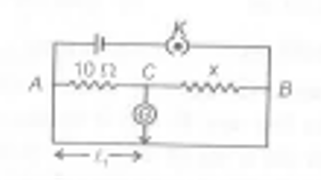 View Solution
View SolutionA copper strip is introduced in the left gap and a resistance R−0.4Ω is placed in the right gap of a meter bridge experiment. The balance points before and after interchanging the copper strip and the resistance R are 30 cm and 60 cm respectively. The resistance per unit length of the bridge wire is
View SolutionA 6Ω resistance is connected in the left gap of a meter bridge. In the second gap 3Ω and 6Ω are joined in parallel. The balance point of the bridge is at _______
View Solution(i) State the principle of working of a meter bridge.
(ii) In a meter bridge balance point is found at a distance I1 with resistances R and S as shown in the figure. When an unknown resistance X is connected in parallel with the resistance S, the balance point shifts to a distance I2. Find the expression for X in terms of l1,l2 and S.View Solution

