Two identical sheets of a metallic foil are separated by d and capacitance of the system is C and charged to a potential difference E. Keeping the charge constant, the separation is increased by 'l'. Then, the new capacitance and potential difference will be
ε0Ad, E
ε0Ad+l, E
ε0Ad+l, (1+ld)E
ε0Ad, (1+ld)E
q=CV=C1V1
when C=ε0Ad and
q=ε0AEd=ε0AE1(d+l)
∴ε0AdE=ε0A(d+l)E1
∴E1=(d+l)d⋅E
=(1+ld)⋅E
and C1=ε0Ad+l
∴(C)
Similar Questions
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
n identical capacitors are connected in parallel to a potential difference V. These capacitors are then reconnected in series, their charges being left undisturbed. The potential difference obtained is
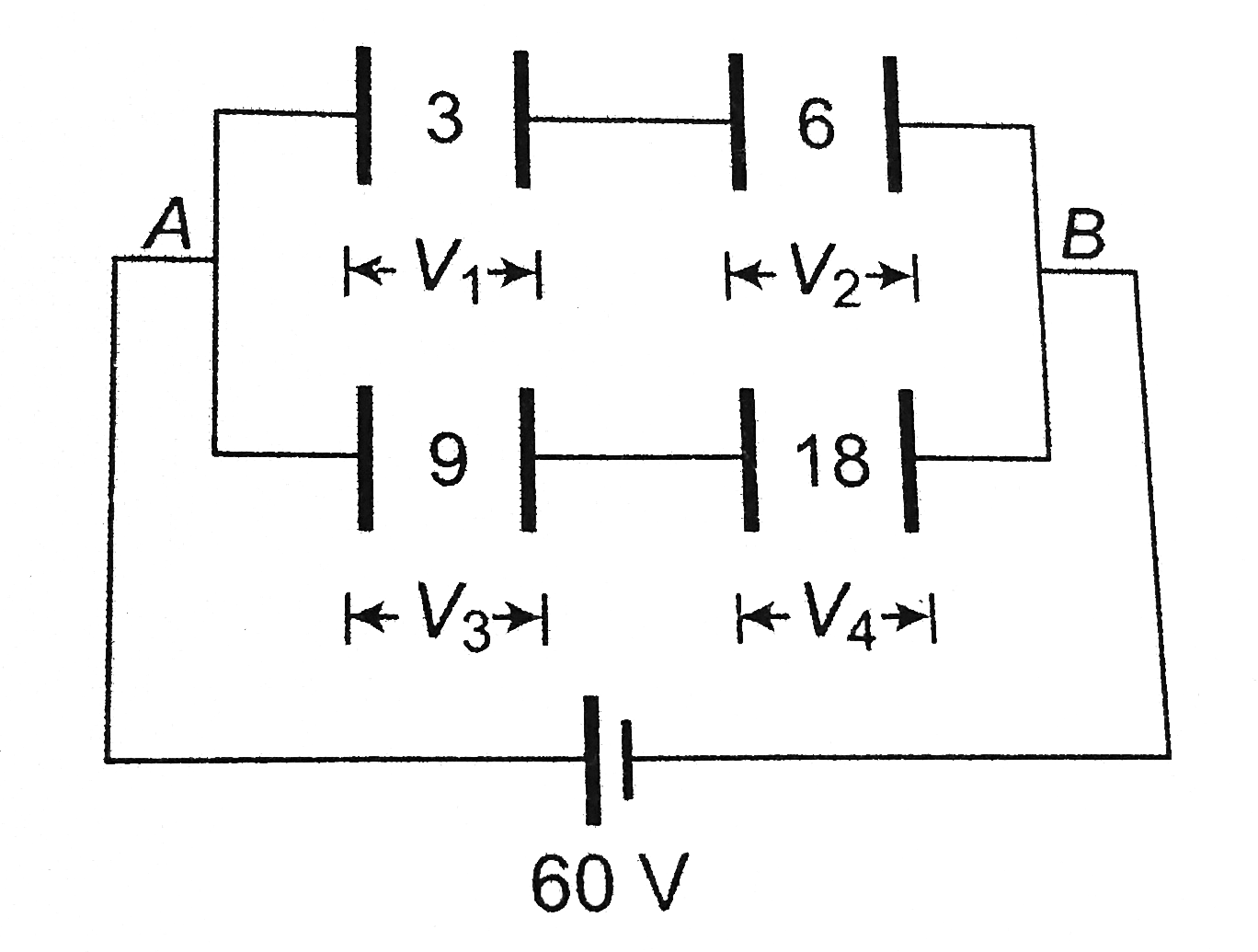
View SolutionFind the potential difference and charge on each capacitance. All capacitances are in μF.
View SolutionWhen the separation between two charges is increased, the electric potential energy of the charges
View SolutionWhen the separation between two charges is increased, the electric potential energy of the charges
View SolutionCharges 2q and −3q are given to two identical metal plates of area of cross section A. the distance between the plates is d. Find the capacitance and potential difference between the plates.
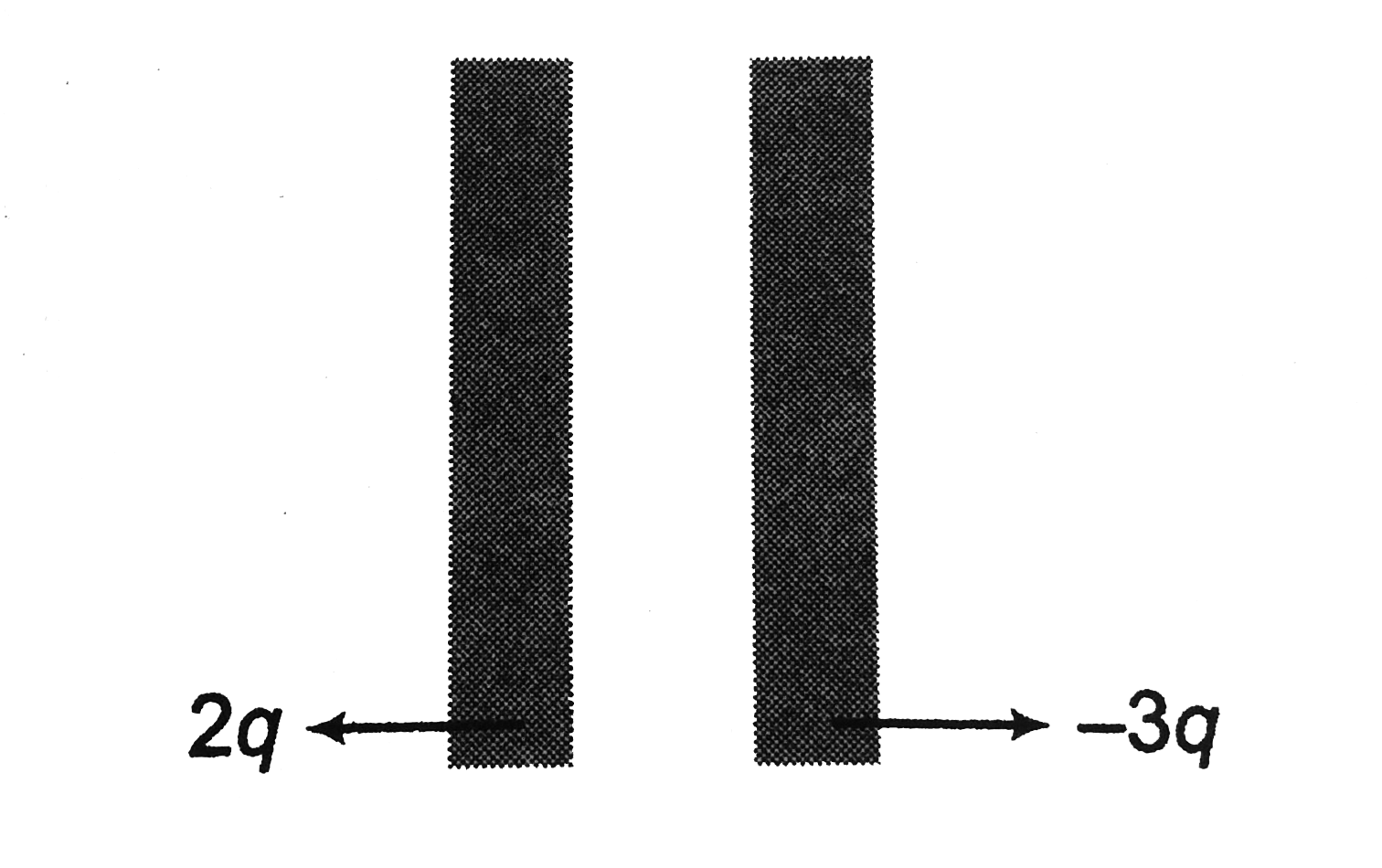
View SolutionA capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
View SolutionA capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
View Solution
