A uniform magnetic field of intensity 1T is applied in a circular region of radius 0.1m, directed into the plane of paper. A charged particle of mass 5×10−5kg and charge q=5×10−4C enters the field with velocity 1/√3m/s making an angle of ϕ with a radial line of circular region in such a way that it passes through centre of applied field the angle ϕ is
60∘
30∘
45∘
90∘
To solve the problem, we need to find the angle ϕ at which a charged particle enters a uniform magnetic field and passes through the center of the field. Here are the steps to arrive at the solution:
Step 1: Understand the Problem
We have a charged particle with mass m=5×10−5kg and charge q=5×10−4C entering a magnetic field of intensity B=1T with a velocity v=1√3m/s. The particle makes an angle ϕ with the radial line of the circular region of radius R=0.1m.
Step 2: Calculate the Radius of the Path
The magnetic force acting on the charged particle provides the centripetal force required for circular motion. We can equate the magnetic force to the centripetal force:
qvB=mv2R0
Rearranging gives us:
R0=mvqB
Step 3: Substitute the Values
Substituting the known values into the equation:
R0=(5×10−5kg)(1√3m/s)(5×10−4C)(1T)
Calculating R0:
R0=5×10−5×1√35×10−4=1√3×0.1=0.1√3≈0.0577m
Step 4: Analyze the Geometry
The particle passes through the center of the magnetic field, and we can visualize the geometry. The angle ϕ is formed between the velocity vector and the radial line from the center of the magnetic field to the point of entry.
Since the particle moves in a circular path, the radius R0 is perpendicular to the radial line at the point of entry. Therefore, we can use trigonometric relationships to find ϕ.
Step 5: Use Trigonometric Relationships
From the geometry, we can write:
sin(90∘−ϕ)=R2R0
Where R is the radius of the circular region (0.1 m). Thus:
sin(90∘−ϕ)=0.1/20.0577
Calculating this gives:
sin(90∘−ϕ)=0.050.0577≈0.866
Step 6: Find ϕ
Since sin(90∘−ϕ)=cos(ϕ):
cos(ϕ)≈0.866
Thus,
ϕ=60∘
Conclusion
The angle ϕ at which the charged particle enters the magnetic field is 60∘.
We have a charged particle with mass m=5×10−5kg and charge q=5×10−4C entering a magnetic field of intensity B=1T with a velocity v=1√3m/s. The particle makes an angle ϕ with the radial line of the circular region of radius R=0.1m.
The magnetic force acting on the charged particle provides the centripetal force required for circular motion. We can equate the magnetic force to the centripetal force:
Substituting the known values into the equation:
The particle passes through the center of the magnetic field, and we can visualize the geometry. The angle ϕ is formed between the velocity vector and the radial line from the center of the magnetic field to the point of entry.
From the geometry, we can write:
Since sin(90∘−ϕ)=cos(ϕ):
The angle ϕ at which the charged particle enters the magnetic field is 60∘.
Similar Questions
A particle of mass 2×10−3 kg, charge 4×10−3C enters in an electric field of 5V/m, then its kinetic energy after 10 s is
View SolutionA charged particle of mass 10−3kg and charge 10−5C enters a magnetic field of induction 1 T. If g=10ms−2, for what value of velocity will it pass straight through the field without deflection?
View Solution
Knowledge Check
- Question 1 - Select One
A circular plane sheet of radius 10 cm is placed in a uniform electric field of 5×105NC−1, making an angle of 60∘ with the field. Calculate electric flux through the sheet.
A1.36×102Nm2C−1B1.36×104Nm2C−1C0.515×102Nm2C−1D0.515×104Nm2C−1
A proton of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B.The radius of curvature of the resulting path is
View SolutionThe figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
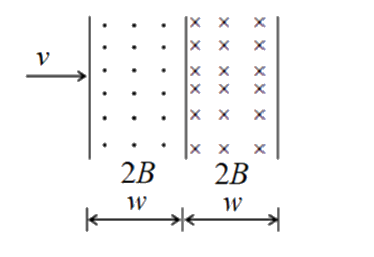 View Solution
View SolutionA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
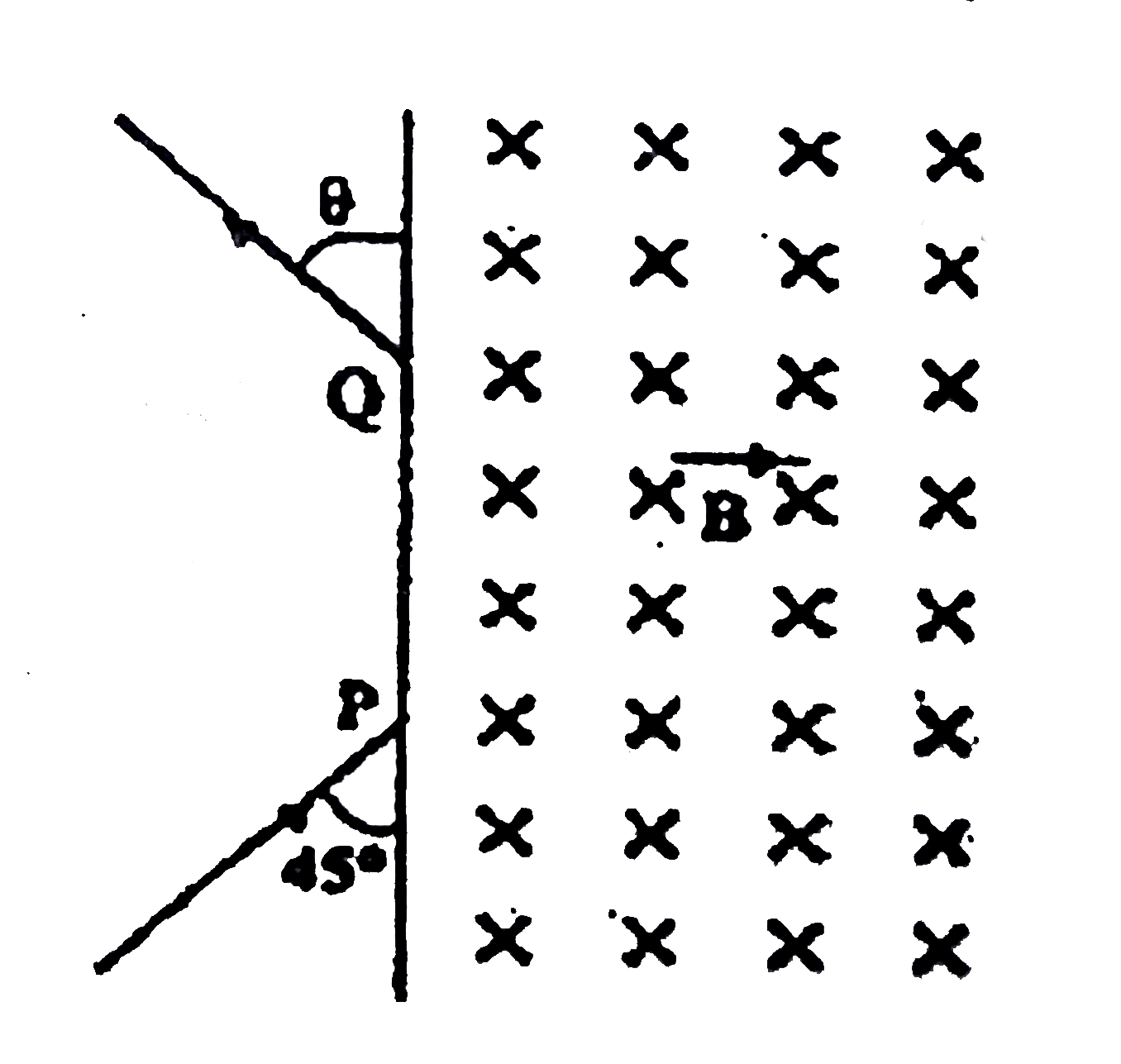 View Solution
View SolutionMagnetic field applied on a cyclotron is 0⋅7T and radius of its dees is 1⋅8m. What will be the energy of the emergent protons in MeV? Mass of proton=1⋅67×10−27kg.
View SolutionMagnetic field applied on a cyclotron is 0⋅7T and radius of its dees is 1⋅8m. What will be the energy of the emergent protons in MeV? Mass of proton=1⋅67×10−27kg.
View SolutionAn electric field is acting vertically upwards . A particle of mass 1 mg and charge −1μC is projected with a velocity 20m/s at an angle 45∘ with the horizontal . Its horizontal range is 10 m, then the intensity of electric field is (g=10m/s2)
View SolutionA beam of protons enters a uniform magnetic field of 0.3T with velocity of 4×105m/s in a direction making an angle of 60∘ with the direction of magnetic field. The path of motion of the particle will be
View Solution

