Use the principle of mathematical induction to show that 52n+1+3n+2.2n−1 divisible by 19 for all natural numbers n.Solution in Kannada
Let P(n)=52n+1+3n+2.2n−1
Step I For n=1,P(1)=52+1+31+2.21−1=125+27=152, which is divisible by 19.
Step II Assume that the result is true for n=k, i.e.,
P(k)=52k+1+3k+2.2k−1 is divisible by 19.
⇒P(k)=19r, where r is an integer .
Step III for n=k+1.
P(k+1)=52(k+1)+1+3k+1+2.2k+1−1
52k+3+3k+3.2k
=25.52k+1+3.3k+2.2.2k−1
=25.52k+1+6.3k+2.2k−1
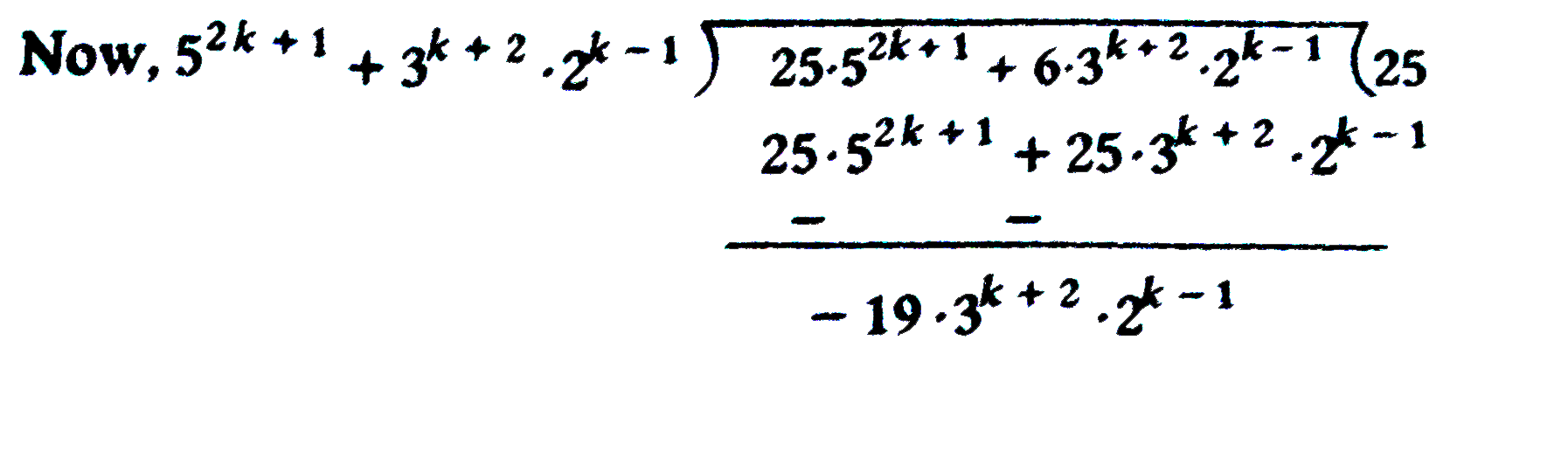
∴25.56(2k+1)+6.3k+2.2k−1=25.(52k+1+3k−2.2k−2)−19.3k+2.2k−1
i.e., P(k+1)=25P(k)−19.3k+2.2k−1
But we know that P(k) is divisible by 19. Also , 19.3k+2.2k−1 is clearly divisible by 19.
Therefore , P(k+1) is divisible by 19. This shows that the result is true for n=k+1.
Hence , by the principle of mathematical induction , the result is true for all n∈N.
Similar Questions
Prove by the principle of mathematical induction that for all n in N.(102n−1+1) is divisible by 11 for all n∈N.
06:57View SolutionProve by the principle of mathematical induction that for all n in N.52n−1 is divisible by 24 for all n∈N.
04:59View SolutionUsing the principle of mathematical induction prove that 32n+1+2n+2is divisible by 7[n∈N]
05:41View SolutionShow by using the principle of mathematical induction that for all natural number n>2,2n>2n+1
04:03View SolutionUsing the Principle of mathematical induction, show that 11n+2+122n+1, where n is a natural number is divisible by 133.
08:11View SolutionUsing principle of mathematical induction, prove that 74n−1 is divisible by 22n+3 for any natural number n.
06:28View SolutionShow by using the principle of mathematical induction that for all natural number n>2,2n>2n+1
02:14View SolutionUsing principle of mathematical induction, prove that 7^(4^(n)) -1 is divisible by 2^(2n+3) for any natural number n.
07:19View Solution

