Show that for a straight conductor, the magnetic field
→B=μoI4πa(cosφ1−cosφ2)ˆn
=μoI4πa(sinθ1+sinθ2)ˆn
Text Solution
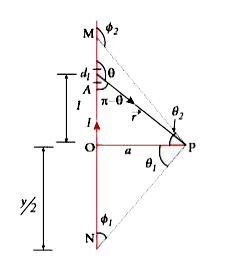
In a right angle triangle OPN, let the angle ∠OPN=θ1 which implies φ1=π2−θ1 and also in a right angle triangle OPM, ∠OPM=θ2 which implies, φ2=π2+θ2
Hence,
→B=μoI4πa(cos(π2−θ1)−cos(π2+θ2))ˆn
=μoI4πa(sinθ1+sinθ2)ˆn
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERT TAMILCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - EVALUATION (I Multiple choice questions)15videos
MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT
- BOOK - NCERT TAMILCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - EVALUATION (IV. Numerical problems)10videos
MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT
- BOOK - NCERT TAMILCHAPTER - ELECTROSTATICSEXERCISE - Exercises23videos
ELECTROSTATICS
- BOOK - NCERT TAMILCHAPTER - MAGNETISM AND MATTEREXERCISE - Additional Exercises19videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
If [1+cosθ+isinθsinθ+i(1+cosθ)]4=cosnθ+isinnθ, then n =
A2B3C4Dnone
If [1+cosθ+isinθsinθ+i(1+cosθ)]4=cosnθ+isinnθ, find n
View SolutionThe value of (1+cosθ+isinθ)n+(1+cosθ−isinθ)n=
View SolutionProve that (1+cosθ+isinθ1+cosθ−isinθ)n=cosnθ+isinnθ
View SolutionProve that the product of matrices [cos2θcosθsinθcosθsinθs∈2θ] and [cos2φcosφsinφcosφsinφs∈2φ] is the null matrix, when θ and φ differ by an odd multiple of π2 .
View SolutionIf sin(πcosθ)=cos(πsinθ) , then show that, θ=±12sin−1(34)
View SolutionIf sin(πcosθ)=cos(πsinθ) ,then prove that : θ=12sin−1(34)
View SolutionThe value of (1+cosθ+isinθ)n+(1+cosθ−isinθ)n=
View Solution
