Let $P (r) = \frac{Q}{π R^{4}} r$ be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'P' inside the sphere at distance $r_{1}$ from the centre of the sphere the magnitude of electric field is

A

$\frac{Q}{4 π \in_{0} r_{1}^{2}}$

B

$\frac{Q r_{1}^{2}}{4 π \in_{0} R^{4}}$

C

$\frac{Q r_{1}^{2}}{3 π \in_{0} R^{4}}$

D

0

Text Solution

Verified by Experts

The correct Answer is:B

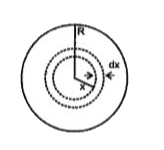
Consider a spherical shell of thickness dx and radius x. The area of this spherical shell = $4 π x^{2} d x$
$[\frac{Q x}{π R^{4}}] 4 π x^{2} d x = \frac{4 Q}{R^{4}} x^{3} d x$
The charge enclosed in a sphere of radius r, is
$= \frac{4 Q}{R^{4}} r_{1} \int 0 x^{3} d x = \frac{4 Q}{R^{4}} {[\frac{x^{4}}{4}]}_{0}^{r_{1}} = \frac{Q}{R^{4}} \times r_{1}^{4}$
$= \frac{1}{4 π ε_{0}} [\frac{Q / R^{4} . r_{1}^{4}}{r_{1}^{2}}]$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Similar Questions

Knowledge Check

Question 1 - Select One
Let $ρ (r) = \frac{Q r}{π R^{4}}$ be the charge density distribution for a soild sphere of radius R and total charge Q. For a point P inside the sphere at a distance $r_{1}$ from the centre of the sphere, the magnitude of electric field is
A $\frac{Q}{4 π ε_{0} r_{1}^{2}}$
B $\frac{Q r_{1}^{2}}{4 π ε_{0} R^{4}}$
C $\frac{Q r_{1}^{2}}{3 π ε_{0} R^{4}}$
Dzero
Question 2 - Select One
Let $ρ (r) = \frac{Q r}{π R^{4}}$ be the charge density distribution for a soild sphere of radius R and total charge Q. For a point P inside the sphere at a distance $r_{1}$ from the centre of the sphere, the magnitude of electric field is
A $\frac{Q r_{1}^{2}}{4 π ε_{0} R^{4}}$
B $\frac{Q r_{1}^{2}}{3 π ε_{0} R_{4}}$
C0
D $\frac{Q}{4 i ε_{0} r_{1}^{2}}$
Question 3 - Select One
Let $p (r) = \frac{Q}{π R^{4}} r$ be the charge JIR density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at distance $z_{1}$ from the centre of the sphere, the magnitude of electric field is
A $\frac{Q r_{1}^{2}}{4 π ε_{0} R^{4}}$
B $\frac{Q r_{1}^{2}}{3 π ε_{0} R_{4}}$
C0
D $\frac{Q}{4 i ε_{0} r_{1}^{2}}$

Recommended Questions

Home
Ask Doubt
Profile