Twelve equal wires each of resistance r are joined to form a skeleton cube. Find the equivalent resistance between two corners on the same edge of the cube.
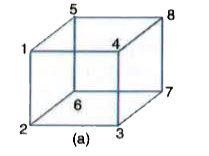
Method-I
Connect a source between points 1 and 2. Let current i enter through point 1 into the network . The network is symmetrical about dotted lines. The currents above and below dotted line are symmetrically distributed as shown in fig.
By junction rule at 1, we have i=x+2y
∴R12=Vi=Vx+2y ....(i)
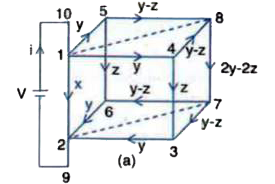
In close loop 1-2-9-10-1 , we have
−rx+V=0 or x=Vr ....(ii)
In close loop 1-4-3-2-1
−rz−rz−ry+rx=0 (or) x−2y−z=0 ....(iii)
In close loop 4−8−7−3−4
−r(y−z)−r×2(y−z)+rz=0
or −4(y−z)+z=0 or 4y+5z=0 ....(iv)
From equations (iii) and (iv) , we get
−4y+5(x−2y)=0 or 5x=14y
Since x=Vr∴y=514×Vr
Now R12=Vx+2y=VVr+2×5V14r=7r12
Method II:
Out previous knowledge reveals that points 3 and 6 must be at the same potential . So must be 4 and 5 . If points of equal potential are joint by a wire, the currents in the circuit do not change. The given network of resistors can be reduced successively as shown in figure.
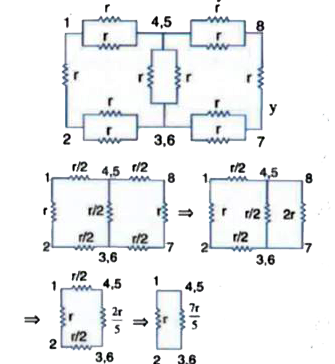
R12=r×7r5r+7r5=712r
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
12 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
12 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
Similar Questions
Twelve identical wires each of resistance 6Ω are joined to from a skeleton cube. Find the resistance between the current of the same edge of the cube
View SolutionTwelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as aandc.

View Solution
Knowledge Check
Twelve equal wires each of resistance rΩ form a cube. The effective resistance between the corners of the same edge of the cube is
A712rB127rC57rD125rTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
A6ΩB12ΩC5ΩD10Ω
Twelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as aandc.

View SolutionEleven equal wires each of resistance r form the edges of a incomplete cube. Find the total resistance from one end of the vacant edge of the cube to the other.
View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and f.

View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and f.

View SolutionTwelve wires of equal resistacne R are connected to form a cube . The effective resistance between two diagonal ends A and E will be .
View SolutionSix wires each of resistance r form a tetrahedron. The equivalent resistance between corners 1-2 and 1-3 are respectively

View Solution
