Calculate the number of half lives elapsed , at the end of which , the activity of a radioactive sample decrease by 90% .
The change in activity with time follows the same law as that of number of radioactive atoms.
∴ Percentage of radioactive atoms left undecayed.
100 - 90% = 10%
i.e., NN0=110 From (NN0)=(12)n
[where n = no . of half lives elapsed]
(12)n=110 or ,2n=10
or n log 2 = log 10 or n=10.3010=3.3
Thus , at the end of 3.3 half lives, the activity (and hence the number of atoms ) would have decreased by 90%.
Similar Questions
Knowledge Check
- Question 1 - Select One
The curve between the activity A of a radioactive sample and the number of active atoms N is.
A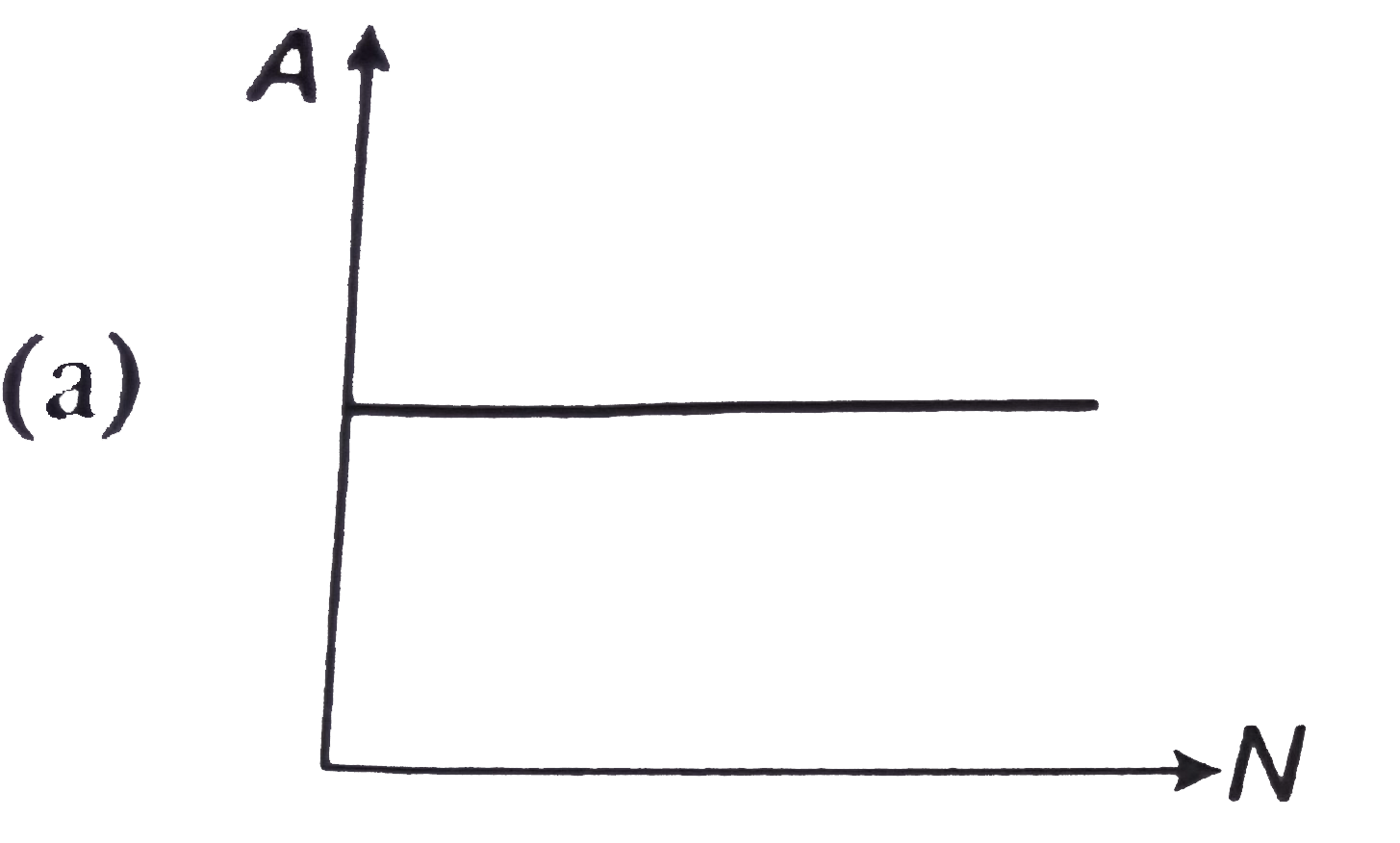 B
B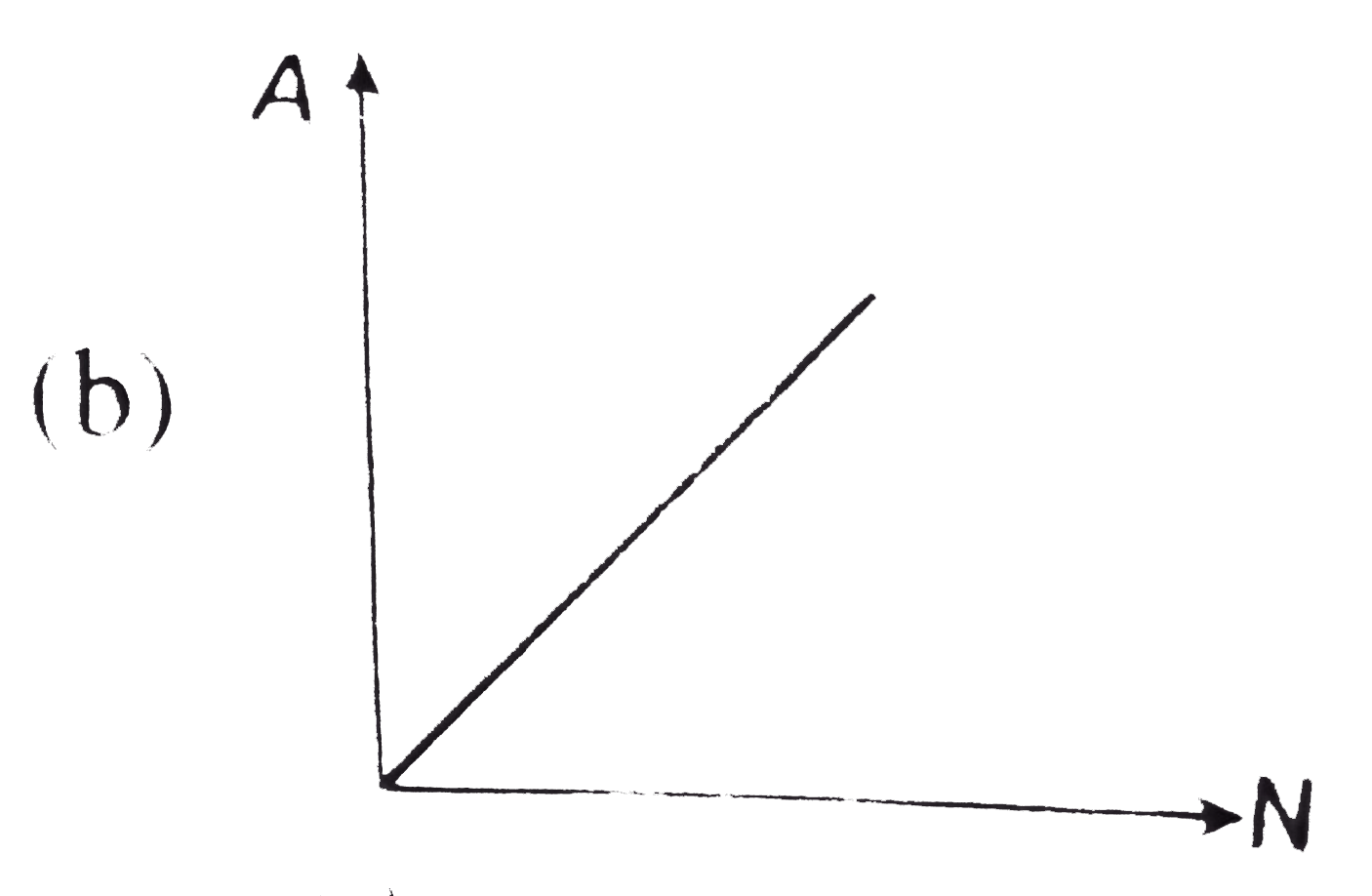 C
C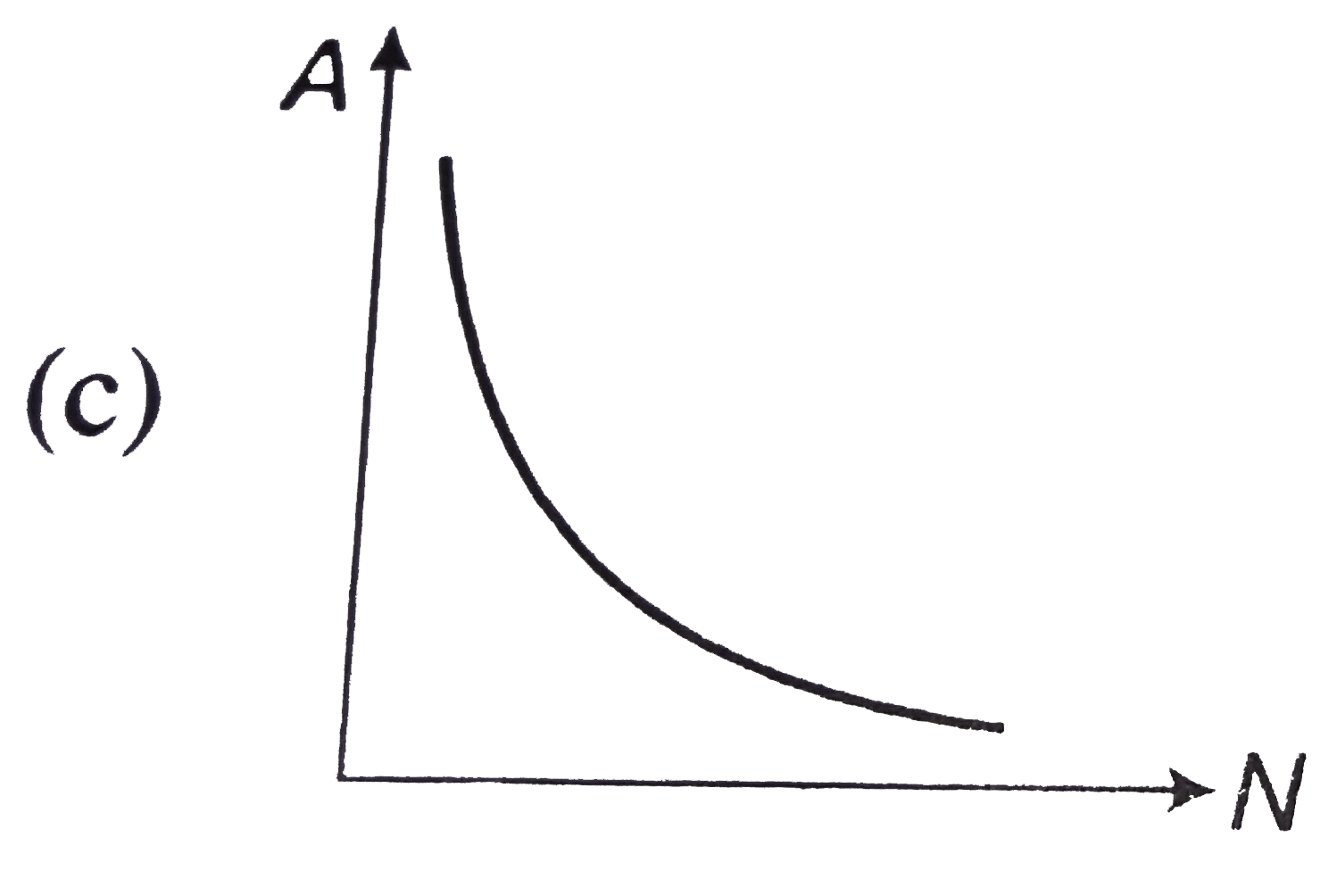 D
D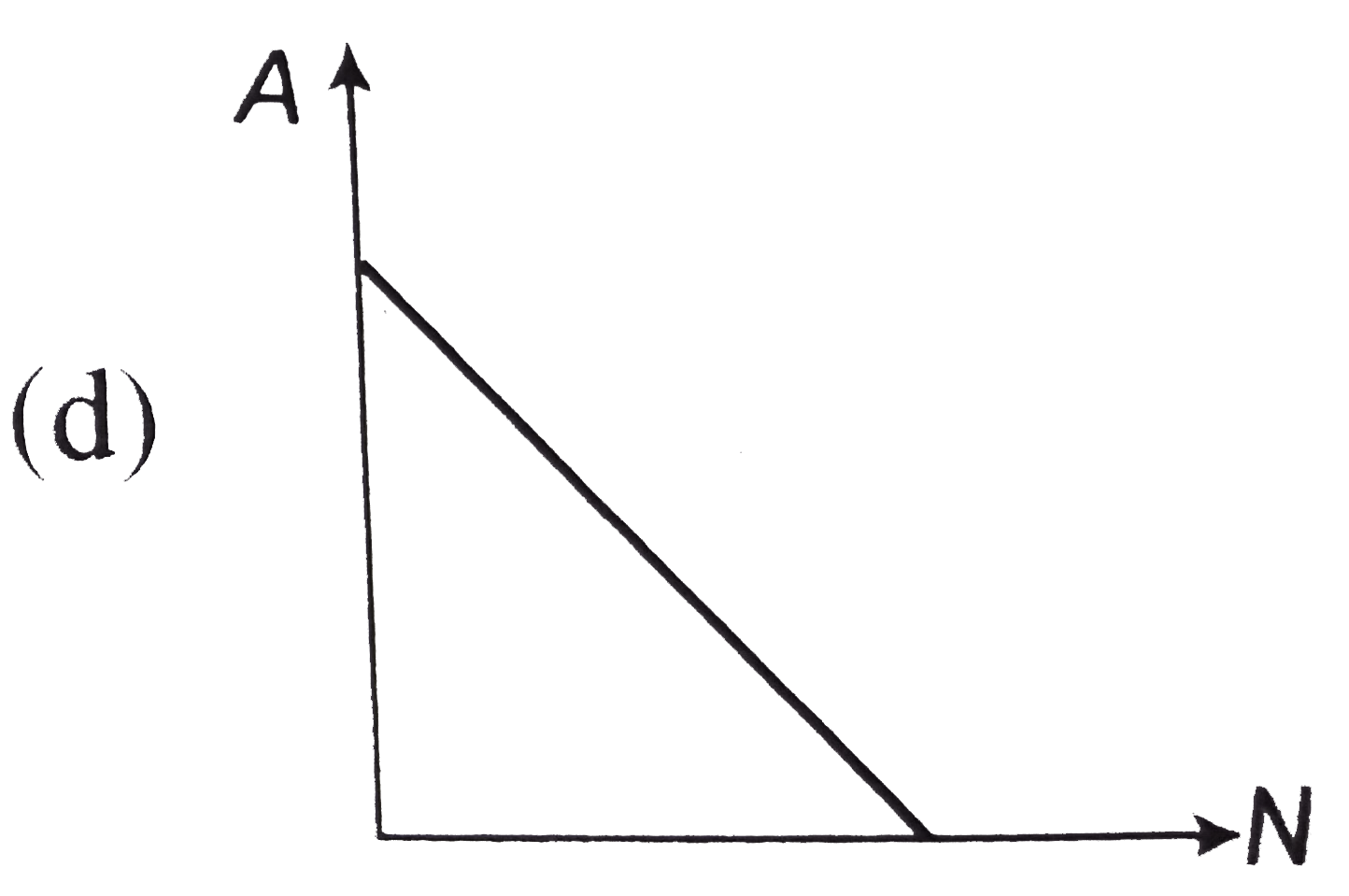
- Question 2 - Select One
Calculate the ratio of half-life to the mean life of a radioactive sample . If λ be the decay constant of a radioactive sample.
A0.693B0.746C1/0.693D(0.693)2 - Question 3 - Select One
A radioactive sample has a half-life of 20 years. The time at which the activity of the sample will reduce to 10% of its initial value is
A75 yB85 yC66 yD45 y
Estimate the number of mean lives elapsed, when the number of atoms in a radioactive sample decrease to 5% of the original value.
View SolutionA radioactive sample has a half-life of 4 years. Calculate the time in which the activity will be reduced to 25%.
View SolutionThe half-life period of a radioactive element is 1.4×1010 years. Calculate the time in which the activity of the element is reduced to 90% of its original value.
View SolutionSTATEMENT-1: The activity of a radioactive sample decreases linearly with time.
STATEMENT-2: The number of active nuclei present in a radioactive sample decreases exponentialy with time.View SolutionA radioactive sample X has thrice the number of nuclei and activity one-third as compared to other radioactive sample Y. The ratio of half-lives of X and Y is
View Solution

