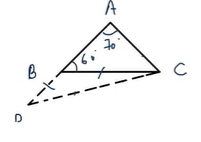
In ΔABC, side AB is produced to D so that BD = BC. If ∠B=60∘and∠A=70∘ then
AD>CD
∠ADC=90∘
AD<CD
∠CAD=30∘
The correct Answer is:A
To solve the problem step by step, we will analyze the triangle ABC and the points defined in the question.
1. Identify the Given Information:
- Triangle ABC with angles:
- ∠A=70∘
- ∠B=60∘
- Side AB is extended to point D such that BD=BC.
2. Calculate Angle C:
- The sum of angles in a triangle is 180∘.
- Therefore, we can find ∠C:
∠C=180∘−∠A−∠B=180∘−70∘−60∘=50∘
3. Determine Angle CBD:
- Since BD=BC, triangle BCD is isosceles.
- The exterior angle ∠CBD can be calculated as:
∠CBD=∠A+∠C=70∘+50∘=120∘
4. Find Angles BDC and BCD:
- In triangle BCD, the angles must sum to 180∘:
∠BDC+∠BCD+∠CBD=180∘
- Substituting ∠CBD=120∘:
∠BDC+∠BCD+120∘=180∘
- This simplifies to:
∠BDC+∠BCD=60∘
- Since ∠BDC=∠BCD (because BD=BC):
2∠BDC=60∘⟹∠BDC=30∘and∠BCD=30∘
5. Analyze Triangle ADC:
- In triangle ADC:
- ∠DAC=70∘
- ∠DCA=∠C+∠BDC=50∘+30∘=80∘
6. Compare Angles and Sides:
- Since ∠DCA=80∘ is greater than ∠DAC=70∘, by the property of triangles, the side opposite to the greater angle is longer.
- Thus, side AD (opposite ∠DCA) is greater than side CD (opposite ∠DAC):
AD>CD
7. Conclusion:
- Therefore, the correct option is that AD is greater than CD.
- Triangle ABC with angles:
- ∠A=70∘
- ∠B=60∘
- Side AB is extended to point D such that BD=BC.
- The sum of angles in a triangle is 180∘.
- Therefore, we can find ∠C:
∠C=180∘−∠A−∠B=180∘−70∘−60∘=50∘
- Since BD=BC, triangle BCD is isosceles.
- The exterior angle ∠CBD can be calculated as:
∠CBD=∠A+∠C=70∘+50∘=120∘
- In triangle BCD, the angles must sum to 180∘:
∠BDC+∠BCD+∠CBD=180∘
- Substituting ∠CBD=120∘:
∠BDC+∠BCD+120∘=180∘
- This simplifies to:
∠BDC+∠BCD=60∘
- Since ∠BDC=∠BCD (because BD=BC):
2∠BDC=60∘⟹∠BDC=30∘and∠BCD=30∘
- In triangle ADC:
- ∠DAC=70∘
- ∠DCA=∠C+∠BDC=50∘+30∘=80∘
- Since ∠DCA=80∘ is greater than ∠DAC=70∘, by the property of triangles, the side opposite to the greater angle is longer.
- Thus, side AD (opposite ∠DCA) is greater than side CD (opposite ∠DAC):
AD>CD
- Therefore, the correct option is that AD is greater than CD.
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 2 EXERCISE - Everyday Mathematics10videos
IMO QUESTION PAPER 2020 SET 2
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 2 EXERCISE - Achievers Section4videos
IMO QUESTION PAPER 2020 SET 2
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Achievers Section5videos
IMO QUESTION PAPER 2020 SET 1
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - ACHIEVERS SECTION (HOTS)5videos
INTRODUCTION TO TRIGONOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
I is the in centre of ΔABC . If ∠BIC=108∘ then ∠A =?
A54∘B72∘C81∘D36∘ - Question 2 - Select One
In ΔABC,BC=ABand∠B=80∘. Then, ∠A=?
A50∘B40∘C100∘D80∘ - Question 3 - Select One
The side BC of Δ ABC is produced to D. If ∠ACD=108∘ and ∠B=12∠A then ∠A is
A36∘B72∘C108∘D59∘
In ΔABC,AB=AC. Side BC is produced to D. Prove that (AD2−AC2)=BD⋅CD.
 View Solution
View SolutionIn a triangle ABC, if AB=AC and AB is produced to D such that BD=BC, find ∠ACD : ∠ADC
View SolutionIn a triangle ABC, AB=BC and ∠A=60∘. Find ∠B.
View SolutionABC is an isosceles triangle with AB = AC. Side BA is produced to D such that AB=AD. Find the ∠BCD:
View SolutionIn ΔABC, AB=AC and D is a point on side AC such that BD = BC, If AB = 12.5 cm and BC = 5 cm, then what is the measure of DC ?
View Solution