A function is matched below against an interval where it is supposed to be increasing. Which of the following parts is incorrectly matched? Interval, Function [2, ∞) , 2x3−3x2−12x+6 (−∞,∞) , x3=3x2+3x+3 (−∞−4) , x3+6x2+6 (−∞,13) , 3x2−2x+1
FunctionIntervalx3+6x2+6(−∞,−4)
FunctionInterval3x2−2x+1(−∞,13)
FunctionInterval2x3−3x2−12x+6[2,∞)
FunctionIntervalx3−3x2+3x+3(−∞,∞)
The correct Answer is:B
Let f(x)=x3+6x2+6……………..i
⇒f'(x)=3x2+12x=3x(x+4)
For f(x) to be increasing f'(x)>0
⇒xε(−∞,−4)∪(0,∞)
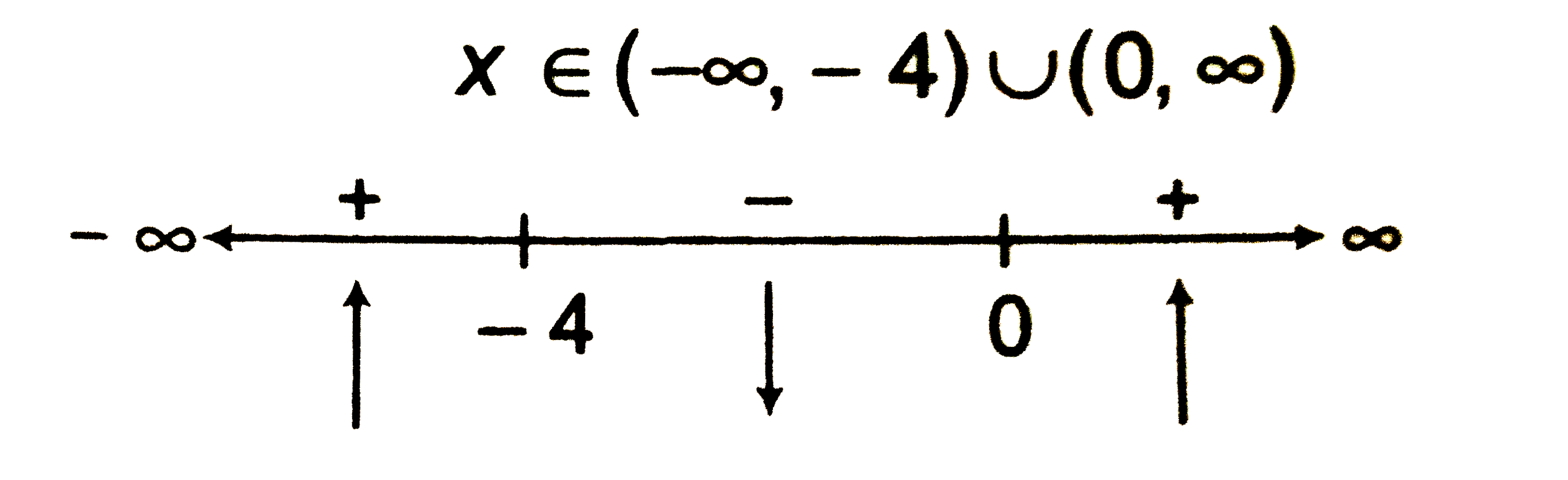
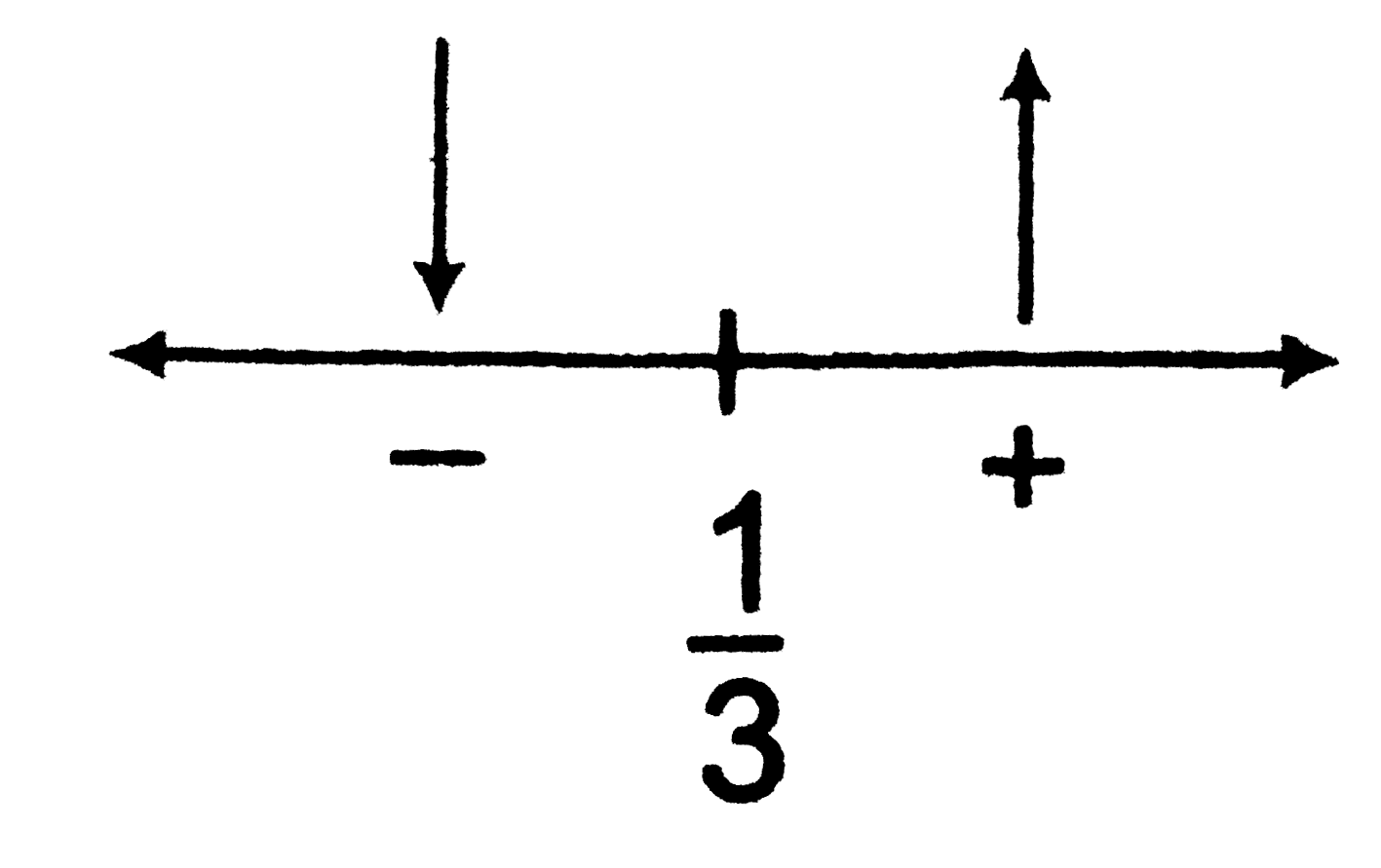
b. Let f(x)=3x2()−2x+1⇒f'(x)=6x−2
For f(x) to be increasing f'(x)>0,
⇒6x−2θ⇒x>13
⇒xε(13,∞)
Hence incorrectly mathced.
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MISCELLANEOUS PROBLEMS80videos
APPLICATIONS OF DERIVATIVES
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER21videos
APPLICATIONS OF DERIVATIVES
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner6videos
APPLICATIONS OF DEFINITE INTEGRALS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - BINOMIAL DISTRIBUTIONEXERCISE - MHT CET Corner6videos
BINOMIAL DISTRIBUTION
Similar Questions
A function is matched below against an interval where it is supposed to be increasing. Which of the following parts is incorrectly matched? Interval, Function (a)[2, ∞) , 2x3−3x2−12x+6 (b)(−∞,∞) , x3=3x2+3x+3 (c)(−∞−4) , x3+6x2+6 (d)(−∞,13) , 3x2−2x+1
View SolutionIf f:(−∞,3]→[7,∞);f(x)=x2−6x+16, then which of the following is true
View Solution
Knowledge Check
- Question 1 - Select One
A continuous and differentiable function f(x) is increasing in (−∞,32) and decreasing in (32,∞) then x=32 is
Apoint if local maximaBpoint of local minimaCpoint of inflectionDNone of these
Find the number of integral vaues of 'a' for which the range of function f(x)=x2−ax+1x2−3x+2is (−∞,∞),
View SolutionThe function f(x)=−2x3+21x2−60x+41,in the interval (−∞,1),
View SolutionIf the function f(x)=2x2−kx+5 is increasing on [1, 2] , then k lies in the interval (a) (−∞, 4) (b) (4, ∞) (c) (−∞, 8) (d) (8, ∞)
View SolutionThe function f(x)=−2x3+21x2−60x+41,in the interval (−∞,1),
View SolutionFind the intervals in which the function f given by f(x)=x2−4x+6 is strictly increasing:
a)(−∞,2)∪(2,∞)
b)(2,∞)
c)(−∞,2)
d)(−∞,2]∪(2,∞)View SolutionFind the intervals in which the function f given by f(x)=x2−4x+6 is strictly increasing:
a)(−∞,2)∪(2,∞)
b)(2,∞)
c)(−∞,2)
d)(−∞,2]∪(2,∞)View SolutionShow that
(a) the function f(x)=x3+3x+5 increase in the entire domain of the definition,
(b) the function g(x)=x(1+x)2 decrease in the interval (1,∞)View Solution

