I-disc
Isotropic disc (light band)
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - LOCOMOTION AND MOVEMENT EXERCISE - SECTION -D Textual Exercise7videos
LOCOMOTION AND MOVEMENT
- BOOK - KUMAR PRAKASHANCHAPTER - LOCOMOTION AND MOVEMENT EXERCISE - SECTION -D Textual Exercise (Fill in the blanks )6videos
LOCOMOTION AND MOVEMENT
- BOOK - KUMAR PRAKASHANCHAPTER - LOCOMOTION AND MOVEMENT EXERCISE - SECTION B (Difference /Scientific Reasons)7videos
LOCOMOTION AND MOVEMENT
- BOOK - KUMAR PRAKASHANCHAPTER - DIGESTION AND ABSORPTIONEXERCISE - Question from Module (Question Paper)11videos
DIGESTION AND ABSORPTION
- BOOK - KUMAR PRAKASHANCHAPTER - MINERAL NUTRITIONEXERCISE - QUESTIONS FOR MODULE (IMPORTANT MCQ FOR NEET)4videos
MINERAL NUTRITION
Similar Questions
The M.I. of a disc of mass M and radius R, about an axis passing through the centre O and perpendicular to the plane of the disc is MR22 . If one quarter of the disc is removed, the new moment of inertia of the disc will be
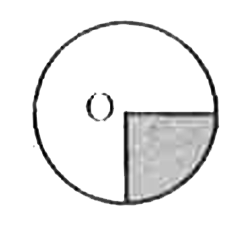 View Solution
View SolutionThe moment of intertia of a disc about an axis passing through its centre and normal to its plane is I. The disc is now folded along a diameter such that the two halves are mutually perpendicular. Its moment of inertia about this diameter will now be
View Solution
Knowledge Check
- Question 1 - Select One
Two uniform circular discs A and B of radii R and 4R with thicknesses x and x/4 respectively, rotate about their axes passing through their centres and perpendicular to their planes. If the M.I. of the first disc is IA and that of the second disc is IB then
AIA=IBBIA>IBCIB>IADData is insufficient - Question 2 - Select One
The M.I. of a disc about its diameter is 2 units. Its M.I. about axis through a point on its rim and in the plane of the disc is
A4 units.B6 units.C8 units.D10 units - Question 3 - Select One
The moment of intertia of a disc about an axis passing through its centre and normal to its plane is I. The disc is now folded along a diameter such that the two halves are mutually perpendicular. Its moment of inertia about this diameter will now be
AIBI√2CI2DI4
Using perpendicular axes theorem, find the M.I. of a disc about an axis passing through its diameter.
View SolutionA circular disc of moment of inertia It is rotating in a horizontal plane about its symmetry axis with a constant angular velocity ωi. Another disc of moment of inertia Ib is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed ωf. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionA circular disc of moment of inertia It is rotating in a horizontal plane about its symmetry axis with a constant angular velocity ωi. Another disc of moment of inertia Ib is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed ωf. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionTwo discs of radii Rand2R are pressed against eachother. Initially, disc wit radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
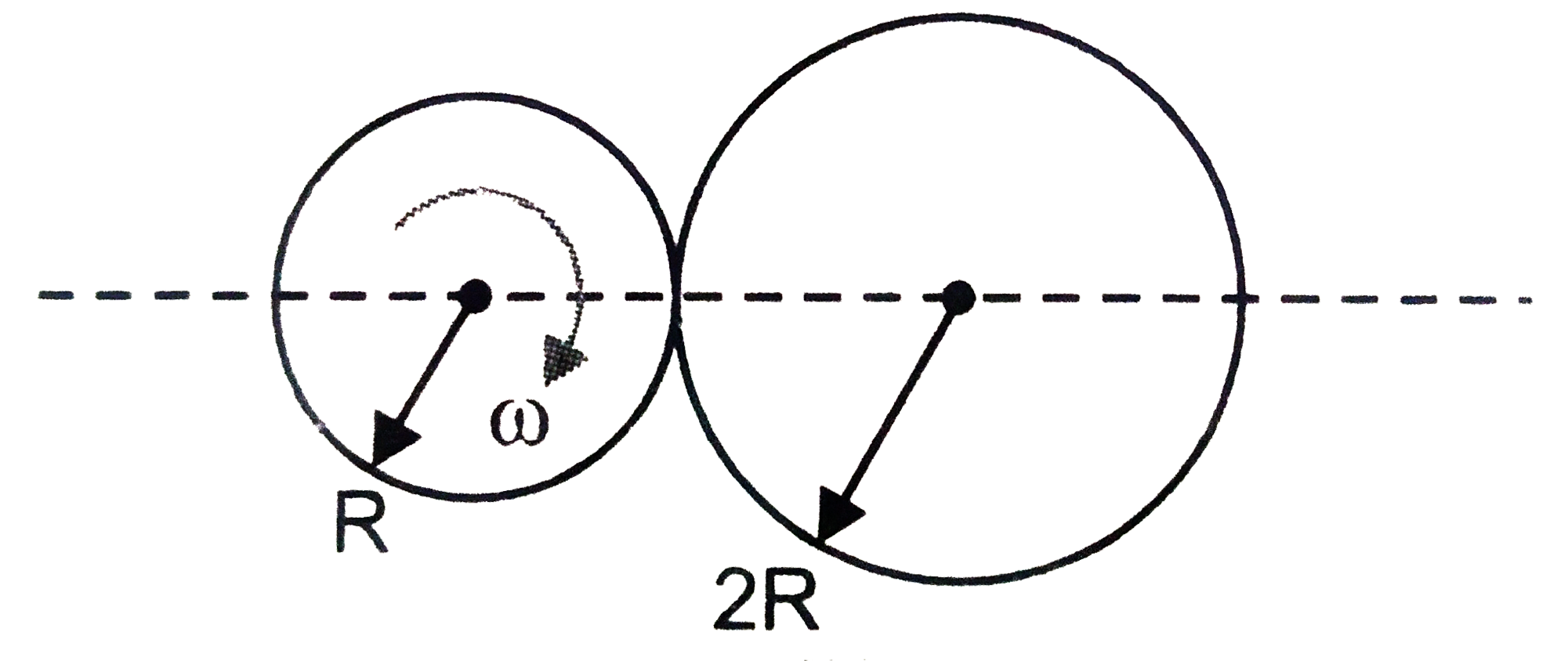 View Solution
View SolutionThe M.I. of disc of mass M and radius 'R' about an axis passing through midway between centre and circumference and perpendicular to its plane is
View Solution

