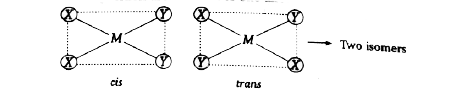
A coordination complex of type MX2Y2 (M-metal ion: X, Y-monodentate lingads), can have either a tetrahedral or a square planar geometry. The maximum number of posible isomers in these two cases are respectively:
1 and 2
2 and 1
1 and 3
3 and 2
The correct Answer is:A
In tetrahedral all the posiiton are adjacent to one another hence only one isomer is possible
Topper's Solved these Questions
- CO-ORDINATION COMPOUNDSBOOK - VK JAISWALCHAPTER - CO-ORDINATION COMPOUNDSEXERCISE - ONE OR MORE ANSWERS IS/ARE CORRECT
72 Videos
- CO-ORDINATION COMPOUNDSBOOK - VK JAISWALCHAPTER - CO-ORDINATION COMPOUNDSEXERCISE - MATCH THE COLUMN
36 Videos
- CHEMICAL BONDING (BASIC)BOOK - VK JAISWALCHAPTER - CHEMICAL BONDING (BASIC)EXERCISE - Level 3 (Passive 11)
6 Videos
- d-BLOCK ELEMENTSBOOK - VK JAISWALCHAPTER - d-BLOCK ELEMENTSEXERCISE - SUBJECTIVE PROBLEMS
6 Videos
Similar Questions
Nickel (Z=28) combines with a uninegative monodentate ligand X− to form a paramagnetic complex [NiX4]2−. The number of unpaired electron(s) in the nickel and geometry of this complex ion are, respectively:
View SolutionFor an octahedral complex MX4Y2 (M=a transition metal, X and Y are monodenate achiral ligands), the correct statement, among the following, is
View Solution
Knowledge Check
A coordination complex of type MX2Y2[M=metal ion, X,Y=monodentata ligands ], can have either a tetrahedral of a square planar geometry. The maximum number of possible isomers in these two cases are respectively
A0 and 2B2 and 1C1 and 3D3 and 2The tetrahedral [CoI4]2− and square planar [PdBr4]2− complex ions are respectively :
Alow spin, high spinBhigh spin, low spinCboth low spinDboth high spinThe tetrahedral [CoI4]2− and square planar [PdBr4]2− complex ions are respectively :
Alow spin, high spinBhigh spin, low spinCboth low spinDboth high spin
Velence bond theroy describes the bonding in complexs in terms of coordinate -covalent bond resulting from overlap filled ligand orbitals with vacant metal hybrid orbitals This theory explains magnetic behaviour and geometrical shape of coordination compounds Magnetic moment of a complex compound can be determined experimentally and theoretically by using spin only formula
Magnetic moment √n(n+2)BM (where n = No. unpaired electrons) .
Ni2+ cation combines with a uninegative monodentate ligand XΘ to form paramagnetic complex [NiCI4]2− The number of unpaired electrons(s) in central metal cation and geometry of this complex respectively are
(a) One,tetrahedral
(b) Two,tetrahedral
(c ) One,square planar
(d) Two, square planar .
View SolutionVelence bond theroy describes the bonding in complexs in terms of coordinate -covalent bond resulting from overlap filled ligand orbitals with vacant metal hybrid orbitals This theory explains magnetic behaviour and geometrical shape of coordination compounds Magnetic moment of a complex compound can be determined experimentally and theoretically by using spin only formula
Magnetic moment √n(n+2)BM (where n = No. unpaired electrons) .
Ni2+ cation combines with a uninegative monodentate ligand XΘ to form paramagnetic complex [NiCI4]2− The number of unpaired electrons(s) in central metal cation and geometry of this complex respectively are
(a) One,tetrahedral
(b) Two,tetrahedral
(c ) One,square planar
(d) Two, square planar .
View SolutionNickel (Z= 28) combines with a uninegative monodentate ligand X− to form a paramagnetic complex [Nix4]2−. The number of unpaired electron(s) in the nickel and geometry of this complex ion are, respectively :
View SolutionNickel (Z=28) combines with a uninegative monodentate ligand X− to form a paramagnetic complex [NiX4]2−. The number of unpaired electron(s) in the nickel and geometry of this complex ion are, respectively:
View SolutionFor the square planar complex [M(a) (b) (c ) (d)] (where M = central metal and a, b, c and d are monodentate ligands), the number of possible geometrical isomers are
View Solution
