At which of the following conditions can a gas be liquified? Tc and Pc are critical temperature and pressure.
T=Tc and P<Pc
T<Tc and P=Pc
T>Tc and P<Pc
T<Tc and P<Pc
To determine the conditions under which a gas can be liquefied, we need to consider the concepts of critical temperature (Tc) and critical pressure (Pc). Here’s a step-by-step solution:
Step 1: Understand Critical Temperature and Pressure
- Critical Temperature (Tc): This is the temperature above which a gas cannot be liquefied, regardless of the pressure applied. If the temperature of the gas is above Tc, it will remain in the gaseous state.
- Critical Pressure (Pc): This is the pressure required to liquefy a gas at its critical temperature. Above this pressure, the distinct phases of liquid and gas do not exist.
Step 2: Conditions for Liquefaction
For a gas to be liquefied, the following conditions must be satisfied:
1. The temperature of the gas must be less than the critical temperature (T < Tc).
2. The pressure of the gas must be greater than or equal to the critical pressure (P ≥ Pc).
Step 3: Analyze the Given Options
Now, we will analyze the options provided in the question based on the conditions derived above.
1. Option 1: Pressure < Pc and Temperature < Tc
- This option cannot liquefy the gas because the pressure is below the critical pressure.
2. Option 2: Pressure = Pc and Temperature < Tc
- This option can liquefy the gas because the pressure is equal to the critical pressure and the temperature is below the critical temperature.
3. Option 3: Pressure < Pc and Temperature > Tc
- This option cannot liquefy the gas because both conditions are not satisfied (pressure is below Pc and temperature is above Tc).
4. Option 4: Pressure < Pc and Temperature < Tc
- This option cannot liquefy the gas because the pressure is below the critical pressure.
Conclusion
Based on the analysis, the only condition under which a gas can be liquefied is in Option 2, where the pressure is equal to the critical pressure and the temperature is less than the critical temperature.
---
- Critical Temperature (Tc): This is the temperature above which a gas cannot be liquefied, regardless of the pressure applied. If the temperature of the gas is above Tc, it will remain in the gaseous state.
- Critical Pressure (Pc): This is the pressure required to liquefy a gas at its critical temperature. Above this pressure, the distinct phases of liquid and gas do not exist.
For a gas to be liquefied, the following conditions must be satisfied:
1. The temperature of the gas must be less than the critical temperature (T < Tc).
2. The pressure of the gas must be greater than or equal to the critical pressure (P ≥ Pc).
Now, we will analyze the options provided in the question based on the conditions derived above.
- This option cannot liquefy the gas because the pressure is below the critical pressure.
- This option can liquefy the gas because the pressure is equal to the critical pressure and the temperature is below the critical temperature.
- This option cannot liquefy the gas because both conditions are not satisfied (pressure is below Pc and temperature is above Tc).
- This option cannot liquefy the gas because the pressure is below the critical pressure.
Based on the analysis, the only condition under which a gas can be liquefied is in Option 2, where the pressure is equal to the critical pressure and the temperature is less than the critical temperature.
Topper's Solved these Questions
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Illustration
2 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises
21 Videos
- SOME BASIC CONCEPTS AND MOLE CONCEPTBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOME BASIC CONCEPTS AND MOLE CONCEPTEXERCISE - Archives Subjective
11 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Answer the following questions based on the p-T phase diagram of carbon dioxide as shown in the figure .
(i) At what temperature and pressure can the solid , liquid and vapour phases of C02 co-exist in equilibrium?
(ii) What is the effect of decrease of pressure on the fusion and boiling point of C02 ?
(iii) What are the critical temperature and pressure for C02 ? what is their significance ?
(iv) Is C02 solid , liquid, or gas at (a) −70∘Cunder 1 atm (b) −60∘C under 10 atm (c) 15∘C under 56 atm ?
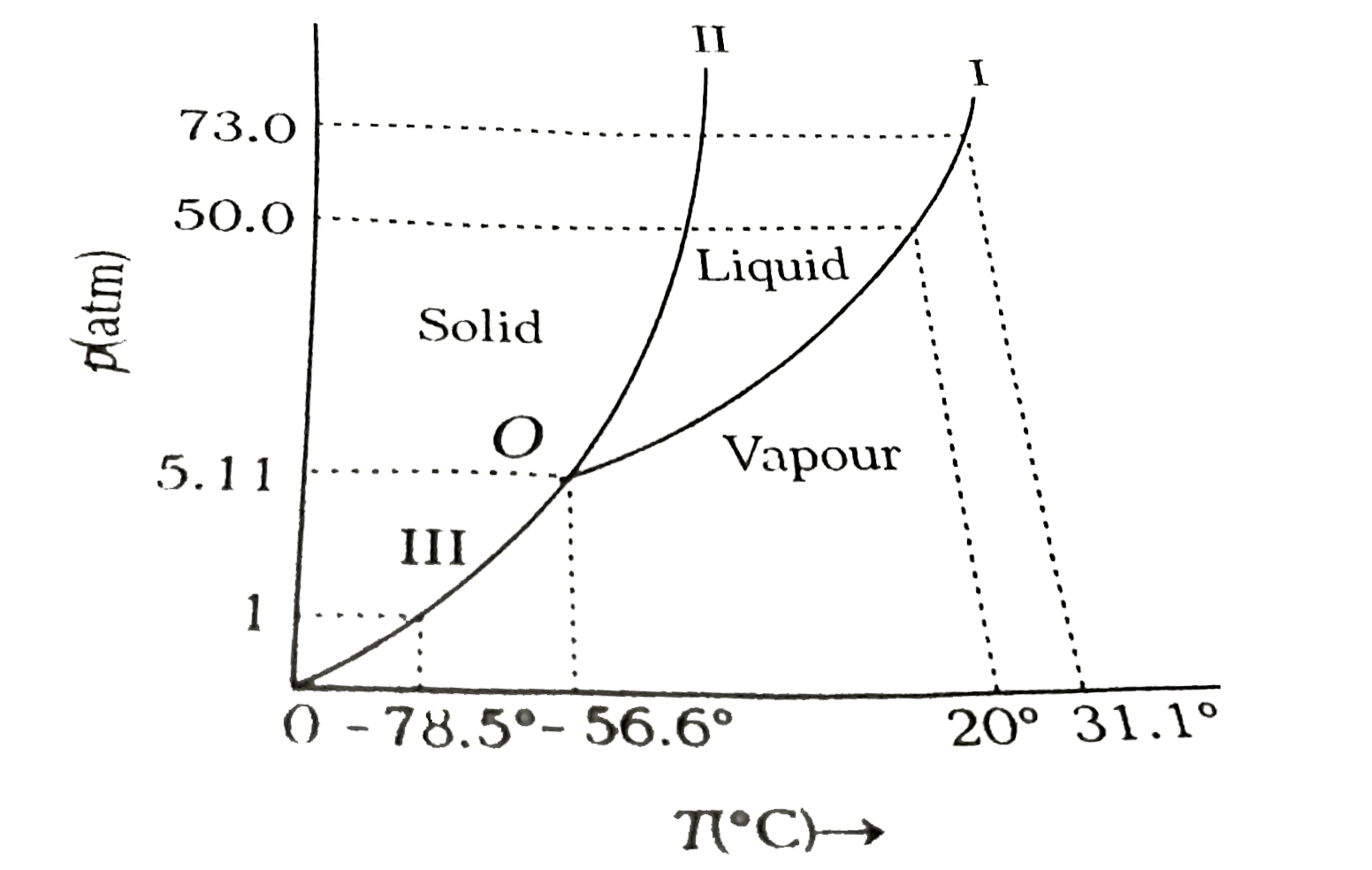
View SolutionAnswer the following questions based on the p-T phase diagram of carbon dioxide as shown in the figure .
(i) At what temperature and pressure can the solid , liquid and vapour phases of C02 co-exist in equilibrium?
(ii) What is the effect of decrease of pressure on the fusion and boiling point of C02 ?
(iii) What are the critical temperature and pressure for C02 ? what is their significance ?
(iv) Is C02 solid , liquid, or gas at (a) −70∘Cunder 1 atm (b) −60∘C under 10 atm (c) 15∘C under 56 atm ?

View SolutionWhich gas can most readly liquified
View SolutionThe essential conditions for liquefaction of gases were discovered by Andrews in 1869 as a result of his study of pressure-volume-temperature relationship for CO2 . It was found that above a certain temperature, it was impossible to liquefy a gas whatever the pressure was applied. The temperature below which the gas can be liquefied by the application of pressure alone is called critical temperature (Tc). The pressure required to liquefy a gas at this temperature is called the critical pressure (Pc). The volume occupied by one mole of the substance at the critical temperature and pressure is called critical volume. Critical constants are related with van der waals' constant as follows:
Vc=3b,Pc=a27b2,Tc=8a27Rb
The values of critical volumes of four gases A, B, C and D are 0.025L, 0.312L, 0.245L and 0.432L respectively. The gas with larger molecular diameter will be :
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionWhich of the following statement (s) is true
I− Slpe of isotherm at critical point is maximum
II− Larger is the value of TC easier is the liquification of gas.
III− Vander walls equation of state is applicable below critical temperature at all pressure.
View SolutionCritical temperature of the gas is the temperature
View SolutionTwo different gases 'A' and 'B' are filled in separate containers of equal capacity under the same condition of temperature and pressure. On increasing the pressure slightly the gas 'A' liquefies but gas B does not liquify even on applying high pressure until it is cooled. Explain this phenomenon.
View SolutionAt which one of the following temperature pressure conditions, the deviation of a gas from ideal behavior is expected to be minimum?
View Solution
