Consider the expression ΔG=−RT In Kp+RT In Qp and select the correct statement at equilibrium
where QpandKp term refer to reaction quotient and eq uilibrium constant at constant pressure respectively.
ΔG=0,Qp>Kp the equilibrium reaction will shift from left to right
ΔG=0,Qp=Kp the equilibrium reaction will shift from left to right
ΔG=∞,Qp<Kp the equilibrium reaction will shift from right to left
ΔG<0,Qp>Kp the equilirbium reaction will shift from right to left
The correct Answer is:B
Van't Hoff reaction isothenn is ΔG=ΔG∘+RT In Qp When the reaction is in a state of equilibrium ΔG=0 M
Then ΔG∘=−RT In Qp=−RT InKp
Topper's Solved these Questions
Similar Questions
Knowledge Check
The relationship between equilibrium constants KpandKc for a gaseous reaction is:
AKp=Kc.R(T)ΔnBKc=Kp.(RT)ΔnCKp=Kc.(RT)ΔnDmol.dm−3For a reaction the free energy change, ΔG=−RT ln Kp+RTlnQp where KP = equilibrium constant, QP= reaction quotient. For the reaction to be in equilibrium state
AQpKp>1BQpKp<1CQpKp=1DQpKp=1For a hypothetical reaction
4A+5B⇔4P+6Q . The equilibrium constant Kc has units.AmolL−1Bmol−1LC(molL−1)−2Dunit less
ΔrG∘=−RT In K. For the same reaction at the same temperature using KcandKp the values ΔrG∘ are found to be different . Why ?
View SolutionThe equilibrium constant Kp for a reaction at "300K" was found to be 104 What will be Δ G∘ for reaction at same temperature
View SolutionThe reaction which is in dynamic equilibrium, ensured us, that the reaction is reversible . But if that the reaction is in equilibrium. The reaction quotient predict either the reversible reaction is in equilibrium or tries to achieve equilibrium. In those reactions which have not achieved equilibrium, we obtain reaction quotient Qc in place of equilibrium constant (Kc) by substituting the concentration of reactant and product at the time, at whih we have to calculate the value of Qc . To determine the direction at which the net reaction will proceed to achieve equilibrium, we compare values of Qc and Kc. The three possible cases are shown as comparison of Kc and Qc in the following figures.

Change in Gibbs free energy, i.e., ΔG is the driving force of any reaction.
For spontaneous reaction , ΔG=−ve
For non-spontaneous reaction , ΔG=+ve
For reaction at equilibrium , ΔG=0
Thermodynamically, we know that
ΔG=ΔG∘+RTlnQ, where Q is reaction quotient and ΔG∘= change in Gibbs energy at standard condition.
For equilibrium A(g)⇔B(g)(Keq=1.732) If the pressure of the system [varied by introducing a stream of A(g) and B (g) is represented by the curve at constant temperature T.
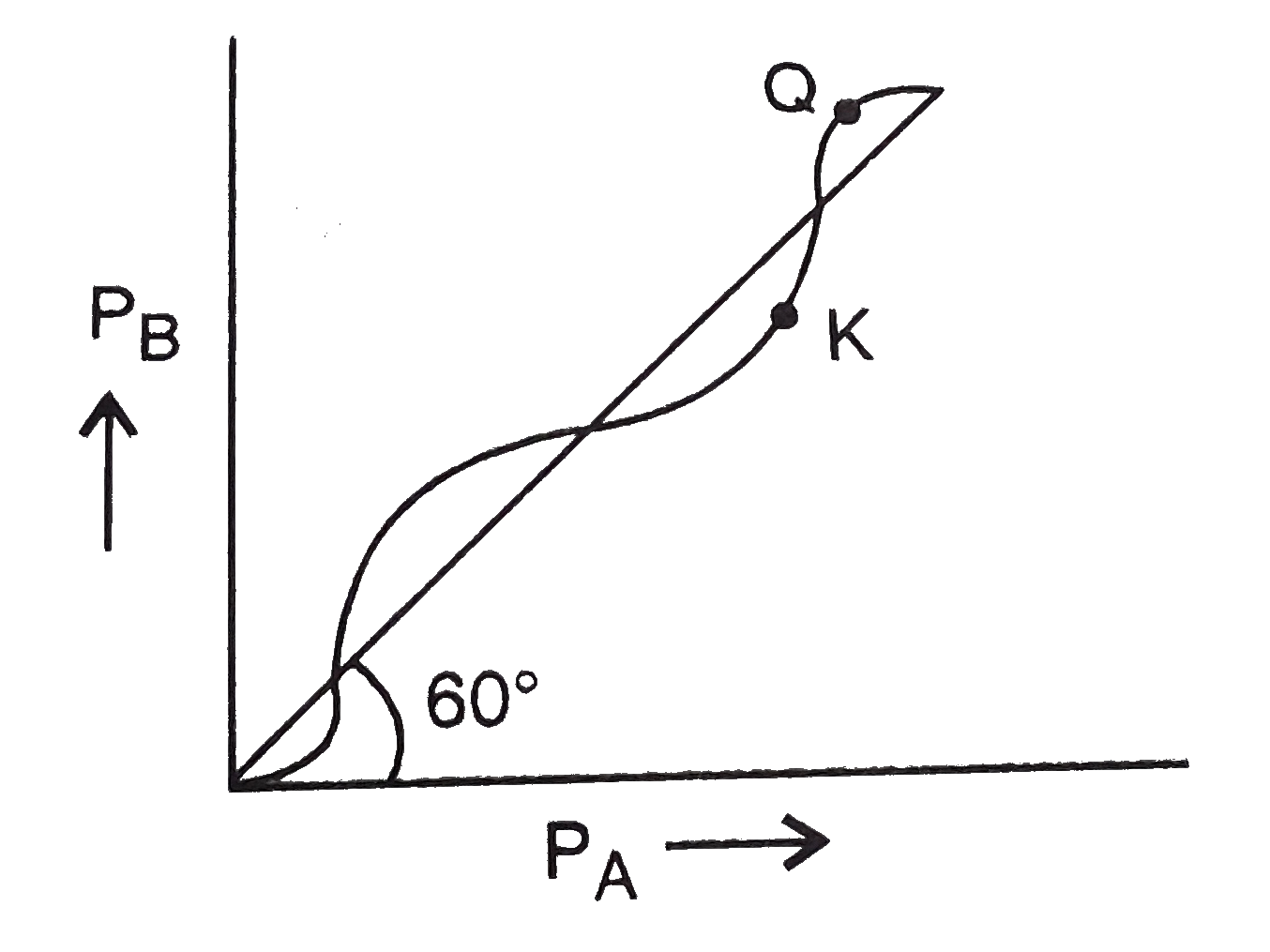
Which of the following is the correct statement at point R in the figure above ?
View SolutionThe reaction which is in dynamic equilibrium, ensured us, that the reaction is reversible . But if that the reaction is in equilibrium. The reaction quotient predict either the reversible reaction is in equilibrium or tries to achieve equilibrium. In those reactions which have not achieved equilibrium, we obtain reaction quotient Qc in place of equilibrium constant (Kc) by substituting the concentration of reactant and product at the time, at whih we have to calculate the value of Qc . To determine the direction at which the net reaction will proceed to achieve equilibrium, we compare values of Qc and Kc. The three possible cases are shown as comparison of Kc and Qc in the following figures.
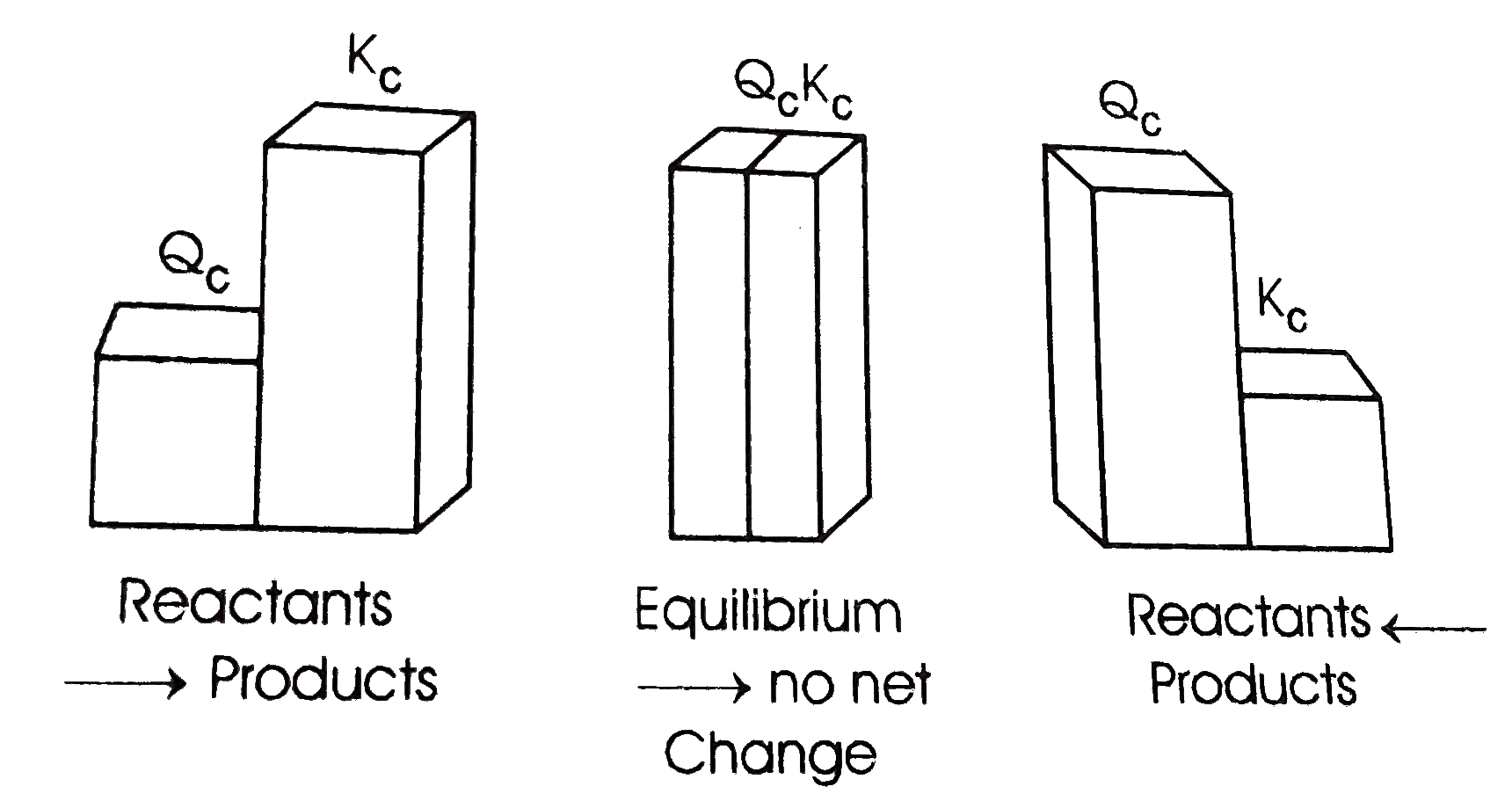
Change in Gibbs free energy, i.e., ΔG is the driving force of any reaction.
For spontaneous reaction , ΔG=−ve
For non-spontaneous reaction , ΔG=+ve
For reaction at equilibrium , ΔG=0
Thermodynamically, we know that
ΔG=ΔG∘+RTlnQ, where Q is reaction quotient and ΔG∘= change in Gibbs energy at standard condition.
For equilibrium A(g)⇔B(g)(Keq=1.732) If the pressure of the system [varied by introducing a stream of A(g) and B (g) is represented by the curve at constant temperature T.
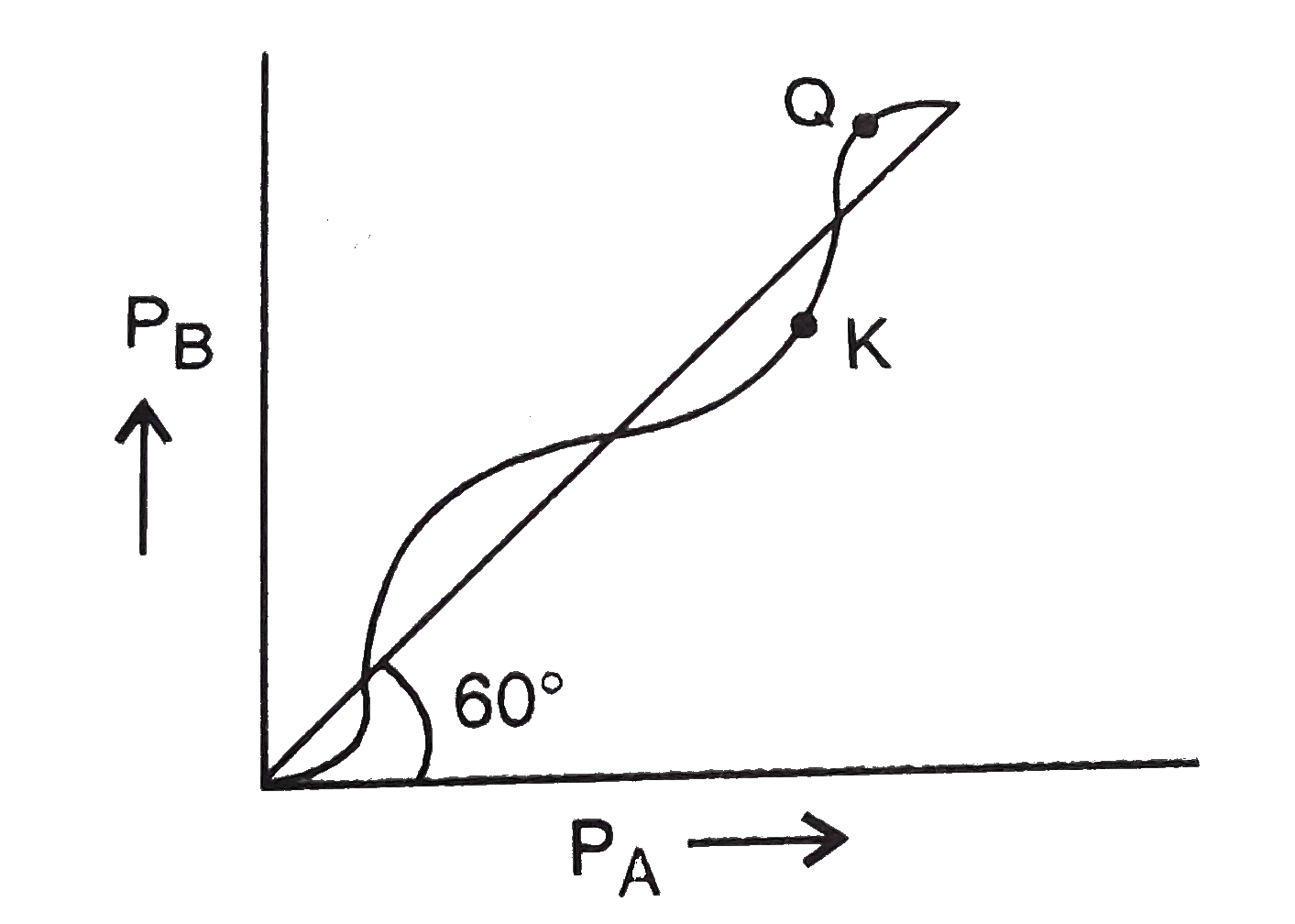
What will be the value of difference of standard Gibbs free energy to Gibbs free energy change at point Q in the figure above ?
View SolutionKp and Kc are inter related as
Kp=Kc(RT)Δn
Answer the following questions:
The unit of equilibrium constant for
H2(g)+I2(g)⇔2HI(g)
View Solution
