Following is the graph between logt1/2 and loga (a initial concentration) for a given reaction at 27∘C.

Find the order of reaction.
The correct Answer is:0
t1/2∝1an−10
t1/2=k.1an−10
logt1/2=logk−(n−1)loga0,[y=c+mx]
tan45∘=1
∴n=0
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Fill In The Blanks
37 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises True/False
29 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Assertion-Reasoning
22 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRYCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
Knowledge Check
Following is the graph between log T50 and log a (a = initial concentration) for a given reaction at 27∘C.
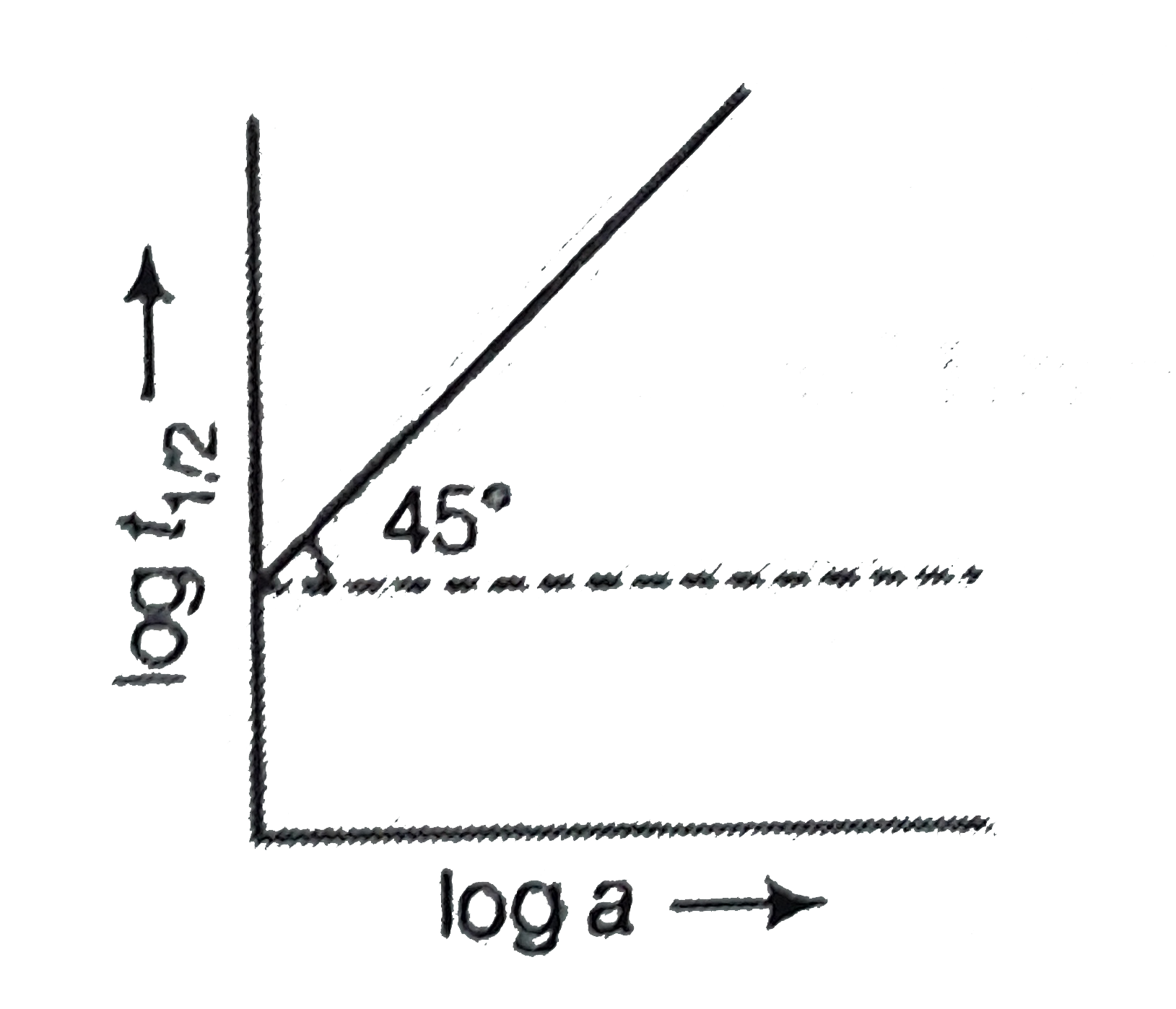
Hence, order isA1B2C3D0Following is the graph between logT50 and loga (a= initial concentration) for a given reaction at 27∘C. Hence order is
 A0B1C2D3
A0B1C2D3The t1/2 of a reaction is halved as the initial concentration of the reactant is doubled then order of reaction :-
A1B0C2D3
A graph between log t1/2 and log a (abscissa), a being the initial concentration of A in the reaction A → product, is depicted in the figure. The rate law is
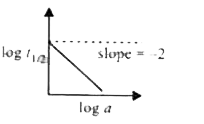
View SolutionIf doubting the initial concentrations of a reactant doubles t12 of the reaction , the order of the reaction is
View SolutionA graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
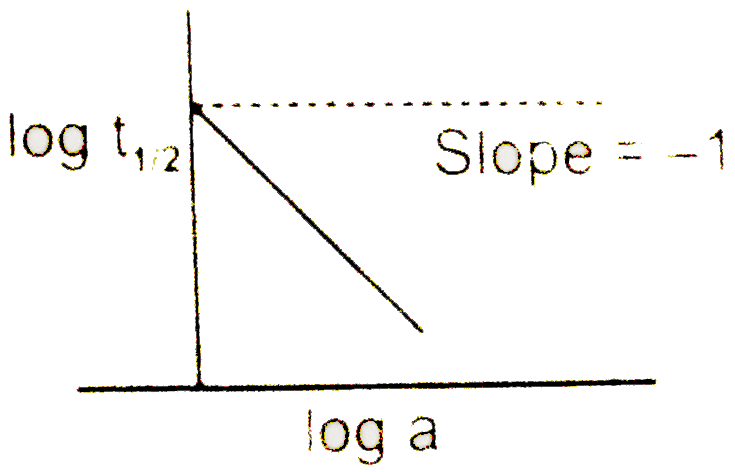
View SolutionThe graph between log t1/2 and log a at a given temperature is
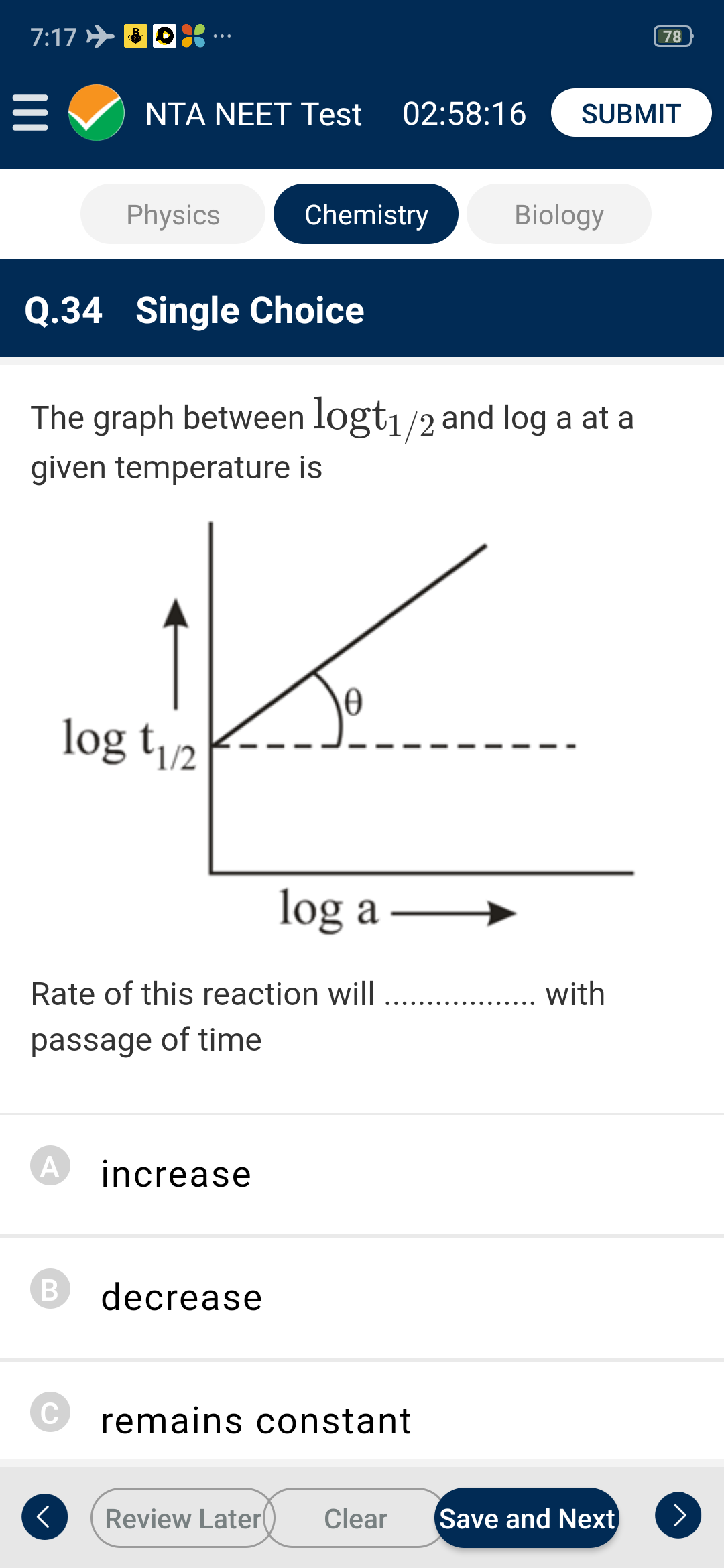
Rate of this reaction will …….with passage of time
View SolutionFrom different sets of data of t1/2 at diifferent initial concentrations say 'a' for a given reaction, the [t1/2×qa] is found to be constant. The order or reaction is :
View Solution
