For the reaction a+b⇔c+d, initially concentrations of a and b are equal and at equilibrium the concentration of will be twice of that of a. What will be equilibrium constant for the reaction ?
2
9
4
3
The correct Answer is:C
To solve the problem step by step, we will analyze the reaction and the given conditions to find the equilibrium constant (K).
1. Write the Reaction:
The reaction is given as:
A+B⇌C+D
2. Define Initial Concentrations:
Let the initial concentrations of A and B be equal, say (A)0=(B)0=a.
The initial concentrations of C and D are zero:
(C)0=(D)0=0
3. Define Changes at Equilibrium:
Let x be the change in concentration of A and B that reacts to form C and D.
At equilibrium, the concentrations will be:
(A)=a−x
(B)=a−x
(C)=x
(D)=x
4. Use the Given Condition:
According to the problem, the concentration of D at equilibrium is twice that of A:
(D)=2(A)
Substituting the expressions we have:
x=2(a−x)
5. Solve for x:
Rearranging the equation:
x=2a−2x
3x=2a
x=23a
6. Substitute x Back into Concentrations:
Now we can find the equilibrium concentrations:
(A)=a−x=a−23a=13a
(B)=a−x=13a
(C)=x=23a
(D)=x=23a
7. Write the Expression for Equilibrium Constant (K):
The equilibrium constant K is given by the formula:
K=(C)(D)(A)(B)
Substituting the equilibrium concentrations:
K=(23a)(23a)(13a)(13a)
8. Simplify the Expression:
K=49a219a2
The a2 terms cancel out:
K=49÷19=4
9. Final Answer:
The equilibrium constant K for the reaction is:
K=4
The reaction is given as:
A+B⇌C+D
Let the initial concentrations of A and B be equal, say (A)0=(B)0=a.
The initial concentrations of C and D are zero:
(C)0=(D)0=0
Let x be the change in concentration of A and B that reacts to form C and D.
At equilibrium, the concentrations will be:
(A)=a−x
(B)=a−x
(C)=x
(D)=x
According to the problem, the concentration of D at equilibrium is twice that of A:
(D)=2(A)
Substituting the expressions we have:
x=2(a−x)
Rearranging the equation:
x=2a−2x
3x=2a
x=23a
Now we can find the equilibrium concentrations:
(A)=a−x=a−23a=13a
(B)=a−x=13a
(C)=x=23a
(D)=x=23a
The equilibrium constant K is given by the formula:
K=(C)(D)(A)(B)
Substituting the equilibrium concentrations:
K=(23a)(23a)(13a)(13a)
K=49a219a2
The a2 terms cancel out:
K=49÷19=4
The equilibrium constant K for the reaction is:
K=4
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - EQUILIBRIUM EXERCISE - HOTS6videos
EQUILIBRIUM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - EQUILIBRIUM EXERCISE - EXEMPLAR PROBLEMS19videos
EQUILIBRIUM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ENVIRONMENTAL CHEMISTRYEXERCISE - Assertion And Reason15videos
ENVIRONMENTAL CHEMISTRY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - HYDROCARBONS EXERCISE - Assertion And Reason15videos
HYDROCARBONS
Similar Questions
A+B⇔C+D. If finally the concentrations of A and B are both equal but at equilibrium concentration of D will be twice of that of A then what will be the equilibrium constant of reaction.
View SolutionA+B⇔C+D. If finally the concentrations of A an d B are both equal but at equilibrium concentration of D will be twice of that of A then what will be the equilibrium constant of reaction.
View SolutionThe equilibrium constant of a chemical reaction
View SolutionThe equilibrium constant for the following reaction is
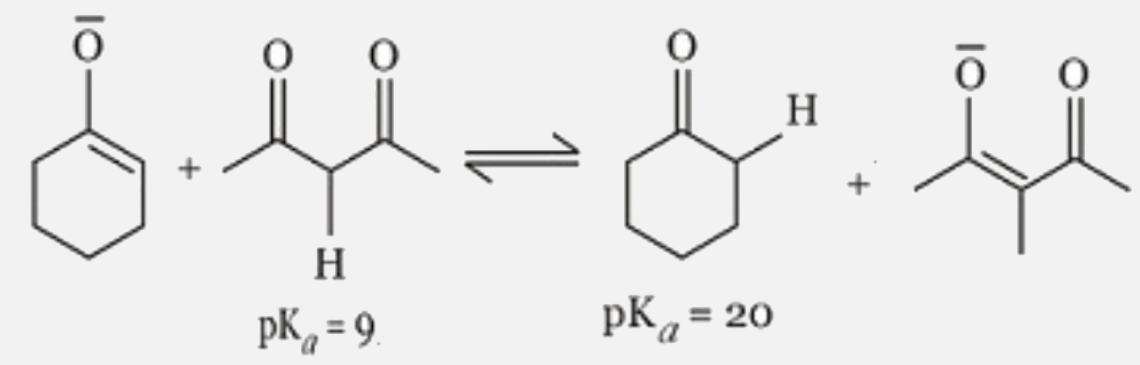 View Solution
View SolutionThe equilibrium constant for the following reaction is
 View Solution
View Solutionfor the reaction P+Q⇒R+2S, initially the concentration of P is equal to that of Q (1 molar) but at equilibrium the concentration of R will be twice of that of P, then the equilibrium constant of the reaction is
View SolutionFor the reaction A+B⇔C+D, the initial concentrations of A and B are equal. The equilibrium concentration of C is two times the equilibrium concentration of A. The value of equilibrium constant is ………..
View SolutionA+B→C+D
Initially moles of A and B are equal. At equilibrium, moles of C are three times of A. The equilibrium constant of the reaction will beView SolutionIf the equilibrium for a reaction is 4.0 what will be the equilibrium constant for the reverse reaction.
View SolutionAt chemical equilibrium , the concentration of all reactants and products are equal
View Solution

