If the radius of the bromide ion is 0.182 nm, how large a cation can fit in each of the tetrahedral holes ?
The correct Answer is:4.01×10−2 nm
To determine the maximum size of a cation that can fit into a tetrahedral hole when given the radius of the bromide ion, we can follow these steps:
Step 1: Understand the relationship between the cation and anion sizes in a tetrahedral void.
In a tetrahedral void, the size of the cation (R+) can be related to the size of the anion (R-) using the formula:
R+R−=k
where k is a constant that varies between 0.225 and 0.414 depending on the specific ionic sizes.
Step 2: Identify the radius of the bromide ion.
Given that the radius of the bromide ion (R-) is:
R−=0.182nm
Step 3: Use the maximum value of k for the calculation.
To find the maximum size of the cation, we will use the upper limit of k, which is 0.414. Thus, we can set up the equation:
R+=k×R−
Step 4: Substitute the values into the equation.
Substituting the values we have:
R+=0.414×0.182nm
Step 5: Perform the calculation.
Now, calculate the value:
R+=0.414×0.182=0.075468nm
Step 6: Round the result to an appropriate number of significant figures.
Rounding the result, we find:
R+≈0.0755nm
Conclusion:
The maximum size of a cation that can fit into the tetrahedral holes is approximately:
R+≈0.0755nm
In a tetrahedral void, the size of the cation (R+) can be related to the size of the anion (R-) using the formula:
R+R−=k
where k is a constant that varies between 0.225 and 0.414 depending on the specific ionic sizes.
Given that the radius of the bromide ion (R-) is:
R−=0.182nm
To find the maximum size of the cation, we will use the upper limit of k, which is 0.414. Thus, we can set up the equation:
R+=k×R−
Substituting the values we have:
R+=0.414×0.182nm
Now, calculate the value:
R+=0.414×0.182=0.075468nm
Rounding the result, we find:
R+≈0.0755nm
The maximum size of a cation that can fit into the tetrahedral holes is approximately:
R+≈0.0755nm
Topper's Solved these Questions
- SOLID STATEBOOK - ICSECHAPTER - SOLID STATEEXERCISE - FOLLOW UP PROBLEMS(Type 1. Calculation of Density of unit cell.)
2 Videos
- SOLID STATEBOOK - ICSECHAPTER - SOLID STATEEXERCISE - FOLLOW UP PROBLEMS(Type II. Calculation of Edge length, Interionic distances and volume of Unit cell.)
4 Videos
- SOLID STATEBOOK - ICSECHAPTER - SOLID STATEEXERCISE - INTEXT QUESTIONS
19 Videos
- SELF ASSESSMENT PAPER-8BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER-8EXERCISE - QUESTIONS
11 Videos
- SOLUTIONSBOOK - ICSECHAPTER - SOLUTIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (Assertion and Reason based questions)
10 Videos
Similar Questions
If the radius of Br− ion is 0.182 nn, how large can a cation be fit in its tetrahedral holes ?
View SolutionIf the radius of Br− ion is 0.20 nn, how large can a cation be fit in its tetrahedral holes ?
View SolutionIf the radius of a Chloride ion is 0.154 nm, then what is the maximum size of a cation that can fit in each of its octahedral voids?
View SolutionThe radius of the bromide ion is 0.182 nm. According to the radius ratio rule the largest cation that can fit in tetrahedral hole has radius
View SolutionBr− ions form close packed structure. If the radius of Br− ion is 195 p, calculate the radius of the cation that just fits in the tetrahedral hole. Can a cation A+ having a radius of 82 pm be slipped into the octahedral hole of the crystal A+Br−?
View SolutionIf the radius of anion is 0.20nm, the maximum radius of cation which can be filleed in respective voids is correctly matched in
View SolutionA crystalline solid AB has NaCl type structure with radius of B− ion is 250 pm. Which of the following cation can be made to slip into tetrahedral site of crystals of A+B− ?
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
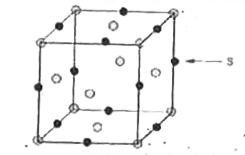
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defect
View Solution
