Neon gas is generally used in the sign boards. If it emits strongly at 616nm, calculate
a. The frequency of emission,
b. The distance traveled by this radiation in 30s
c. The energy of quantum and
d. The number of quanta present if it produces 2J of energy.
Wavelength of radiation emitted = 616 nm=616×10−9 m (Given)
(a) Frequency of emission (v)
v=(c).λ
c = velocity of radiation
λ= wavelength of radiation
Substituting the values in the given expression of (v) :
v=3.0×108m/s616×10−9m
=4.87×108×109×10−3s−1
v=4.87×1014s−1
Frequency of emission (v)=4.87×1014s−1
(b) Velocity of radiation, (c).=3.0×108ms1
Distance travelled by this radiation in 30 s
=(3.0×108ms−1)(30s)
=9.0×109m
(c). Energy of quantum (E)=hν
(6.626×10−34Js)(4.87×1014s−1)
Energy of quantum (E)=32.87×10−20J
(d) Energy of one photon (quantum) =32.27×10−20J
Therefore, 32.27×10−20J of energy is present in 1 quantum.
Number of quanta in 2 J of energy
=2J32.27×10−20J
=6.19×1018
=6.2×1018
Topper's Solved these Questions
Similar Questions
Neon gas is generally used in the sign boards. If it emits strongly at 616nm, calculate
a. The frequency of emission,
b. The distance travelled by this radiation in 30s
c. The energy of quantum and
d. The number of quanta present if it produces 2J of energy.
View SolutionInfrared lamps are used in restaurants to keep the food warm. The infrared radiation is strongly absorbed by water, raising its temperature and that of the food. If the wavelength of infrared radiationis assumed to be 1500 nm, and the number of quanta of infrared radiation produced per second by an infrared lamp (that consumes enregy at the rate of 100 W and is 12% effcient only) is (×1019, then the value of x is :
(Given:h=6.665×10−34J−s)
View Solution
Knowledge Check
Neon gas emits at 616 nm. The distance travelled by this radiation in 30 sec is.
A9×107mB9×109mC4.5×109mD7×109mParamagnetism is a property due to the presence of unpaired electrons. In case of transition metals, as they contain unpaired contain unpaired electrons in the (n−1) d orbitals , most of the transition metal ions and their compounds are paramagnetic . Paramagnetism increases with increases in number of unpaired electrons. Magnetic moment is calculated from 'spin only formula' Vz
μ=√n(n+2)B.Mn=number of unpaired electrons
Similarly the colour of the compounds of transition metals may be attributed to the presence of incomplete (n−1) d sub-shell. When an electron from a lower energy of d-orbitals is excited to a higher energy d-orbital, the energy of excitation corresponds to the frequency of light absorbed. This frequency generally lies in the visible region. The colour observed corresponds to complementry colour of the light obserbed. The frequency of the light absorbed is determined by the nature of the ligand.
Titanium shows magnetic moments of 1.73BM in its compound. What is the oxidation state of titanium in the compound?A+2B+1C+3D+4Paramagnetism is a property due to the presence of unpaired electrons. In case of transition metals, as they contain unpaired electrons in the (n-1)d orbitals, most of the transition metal ions and their compounds are paramagnetic. Paramagnetism increases with increases in number of unpaired electrons. Magnetic moment is calculated from 'Spin only formula' viz.
μ=√n(n+2)B.M.n=no. of unpaired electrons
Similarly the colour of the compounds of transition metals may be attributed to the presence of incomplete (n-1)d subshell. When an electron from a lower energy of d-orbital is excited to a higher energy d-orbital, the energy of excitation corresponding to the frequency of light absorbed. This frequency generally lies in the visible region. The colour observed correponds to complementary colour of the light absorbed. The frequency of the light absorbed is determined by the nature of the ligand.
Titanium shows magnetic moment of 1.7BM in its compound. What is the oxidation state of titanium in the compound?A+2B+1C+3D+4
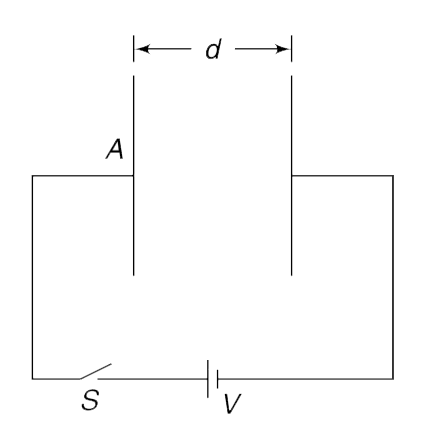
A parallel plate air capacitor has plate area A and separation between the plates d. Switch S is closed to connect the capacitors to a cell of emf V.
(a) Calculate the amount of heat generated in the circuit as the capacitor gets charged.
(b) Calculate the force (F) that one capacitor plate exerts on the other. (c) The distance between the plates is slowly reduced to d2. Calculate the work done by the external agent in the process. For your calculation use the basic definition of work as work = force × displacement.
(d) How much energy is dissipated in the circuit as the distance between the plates is reduced from d to d2 ? Try to give answer without any calculations. Give reasons. Now use work energy theorem to show that your answer is right.
View Solution(a) (i) Find the wavelength of the radiation required to excite thye elctron in Li(++) from the first to the third Bohr orbit.
(ii) How many spectal lines are observed in the emission spectrum of the above excited system ?
(b) The energy needed to detach the electron of a hydrogen-like ion in ground state in 4 rydberg.
(i) What is the wavelength of the radiation emitted when the electron jumps from the first excited state ot the ground state ?
(ii) What is the radius of first orbit ?
(c ) A hydrogen sample is prepared in a particular excited state A. Photons of energy 2.55 eV get absorbed into the sample to take some electrons to a further excited state B. Find the quantum number of the A and B.
(d) A hydrogen atom in a state having a binding energy of 0.85 eV makes transition to a state with excitation energy 10.2 eV. (i) Identify the quantum number n of the upper and the lower energy states.
Find λ.
View SolutionQuantum Numbers
The whereabouts and characteristics of an electron in an atom can be known by a set of four quantum numbers, which describe the electron's distance from nucleus, shape of the orbital, its orientation, and spin.
Principal quantum number (n): The principal quantum number (n) is a positive integer (n = 1, 2, 3, 4, ...) on which the size and energy level of the orbital primarily depends. Its value gives us the 'shell in which the electron is present. It also gives us an idea of the average energy possessed by an electron and the average distance from the nucleus where it is likely to be found.
Azimuthal quantum number (l): The azimuthal quantum number defines the three-dimensional shape of the orbital (subshell) in which the electron is present. Its value ranges from 0 to n-1 for a given value of n, for example, if n = 2, possible values of l are 0 and 1. The azimuthal quantum number is also known as the angular momentum quantum number, and it gives an idea about the absolute value of energy possessed by the electron.
For example, an orbital with n= 3 and l= 2 in the 3d orbital, n = 3 represents the 3rd shell and l = 2 represents the d subshell (if l = 0, 1, 2, and 3, the orbital is s, p, d, and f, respectively).
Magnetic quantum number (m): The magnetic quantum number defines the spatial orientation of the orbital with respect to a standard set of coordinate axes. For an orbital whose angular momentum quantum number is l, the magnetic quantum number m can have values ranging from −l to +l, including 0. Thus, within each subshell (orbitals with the same value of l) there are 2l+1 different spatial orientations for those orbitals.
For example, if l=0, then m= 0.
If l=1, then m = -1, 0, or +1.
If l=2, then m=−2,−1,0,+1,or+2.
If l=3, thenm=−3,−2,−1,0,+1,+2,or+3... and so forth.
Spin quantum number(s): The spin quantum number exemplifies the spin of an electron around its imaginary axis. For each value of magnetic quantum number, only two values of the spin quantum number are permitted, that is,+12or−12,s=+12 denotes a clockwise spin and −12 denotes anticlockwise spin. A maximum of only 2 electrons can be accommodated in each of the spatial orientations represented by m.
Based on the provided information, answer the following questions:
If the principal quantum number is 3, what possible values can azimuthal quantum number have?
View SolutionParamagnetism is a property due to the presence of unpaired electrons. In case of transition metals, as they contain unpaired contain unpaired electrons in the (n−1) d orbitals , most of the transition metal ions and their compounds are paramagnetic . Paramagnetism increases with increases in number of unpaired electrons. Magnetic moment is calculated from spin only formula' Vz
μ=√n(n+2)B.Mn=number of unpaired electrons
Similarly the colour of the compounds of transition metals may be attributed to the presence of incomplete (n−1) d sub-shell. When an electron from a lower energy of d-orbitals is excited to a higher energy d-orbital, the energy of excitation corresponds to the frequency of light absorbed. This frequency generally lies in the visible region. The colour observed corresponds to complementry colour of the light obserbed. The frequency of the light absorbed is determined by the nature of the ligand.
Which of the following pair of Compounds is expected to exhibit same colour in aqueous solution
View SolutionParamagnetism is a property due to the presence of unpaired electrons. In case of transition metals, as they contain unpaired electrons in the (n-1)d orbitals, most of the transition metal ions and their compounds are paramagnetic. Paramagnetism increases with increases in number of unpaired electrons. Magnetic moment is calculated from 'Spin only formula' viz.
μ=√n(n+2)B.M.n=no. of unpaired electrons
Similarly the colour of the compounds of transition metals may be attributed to the presence of incomplete (n-1)d subshell. When an electron from a lower energy of d-orbital is excited to a higher energy d-orbital, the energy of excitation corresponding to the frequency of light absorbed. This frequency generally lies in the visible region. The colour observed correponds to complementary colour of the light absorbed. The frequency of the light absorbed is determined by the nature of the ligand.
Which of the following pair of compounds is expected to exhibit same colour in aqueous solution.
View Solution
