24 12Mgand26 12Mg are symbols of two isotopes of magnesium.
Give reasons why the two isotopes of magnesium have different mass numbers.
To explain why the two isotopes of magnesium, represented as 2412Mg and 2612Mg, have different mass numbers, we can follow these steps:
1. Understanding Isotopes:
- Isotopes are atoms of the same element that have the same number of protons but different numbers of neutrons. This results in different mass numbers.
2. Identifying Atomic Number and Mass Number:
- The atomic number (Z) of magnesium is 12, which means every magnesium atom has 12 protons.
- The mass number (A) is the total number of protons and neutrons in the nucleus of an atom.
3. Calculating Neutrons in Magnesium Isotopes:
- For the isotope 2412Mg:
- Mass number A=24
- Number of protons (atomic number) = 12
- Number of neutrons = Mass number - Number of protons = 24−12=12
- For the isotope 2612Mg:
- Mass number A=26
- Number of protons (atomic number) = 12
- Number of neutrons = Mass number - Number of protons = 26−12=14
4. Conclusion:
- The two isotopes of magnesium have different mass numbers because they contain different numbers of neutrons. 2412Mg has 12 neutrons, while 2612Mg has 14 neutrons. This difference in neutron count leads to the difference in their mass numbers.
Summary:
- The isotopes 2412Mg and 2612Mg differ in mass numbers due to the difference in the number of neutrons (12 neutrons in 24 and 14 neutrons in 26).
- Isotopes are atoms of the same element that have the same number of protons but different numbers of neutrons. This results in different mass numbers.
- The atomic number (Z) of magnesium is 12, which means every magnesium atom has 12 protons.
- The mass number (A) is the total number of protons and neutrons in the nucleus of an atom.
- For the isotope 2412Mg:
- Mass number A=24
- Number of protons (atomic number) = 12
- Number of neutrons = Mass number - Number of protons = 24−12=12
- For the isotope 2612Mg:
- Mass number A=26
- Number of protons (atomic number) = 12
- Number of neutrons = Mass number - Number of protons = 26−12=14
- The two isotopes of magnesium have different mass numbers because they contain different numbers of neutrons. 2412Mg has 12 neutrons, while 2612Mg has 14 neutrons. This difference in neutron count leads to the difference in their mass numbers.
- The isotopes 2412Mg and 2612Mg differ in mass numbers due to the difference in the number of neutrons (12 neutrons in 24 and 14 neutrons in 26).
Topper's Solved these Questions
- ATOMIC STRUCTURE AND CHEMICAL BONDINGBOOK - ICSECHAPTER - ATOMIC STRUCTURE AND CHEMICAL BONDINGEXERCISE - EXERCISE 4(D)
21 Videos
- ATOMIC STRUCTURE AND CHEMICAL BONDINGBOOK - ICSECHAPTER - ATOMIC STRUCTURE AND CHEMICAL BONDINGEXERCISE - EXERCISE 4(B)
12 Videos
- ATMOSPHERIC POLLUTIONBOOK - ICSECHAPTER - ATMOSPHERIC POLLUTIONEXERCISE - EXERCISE 8(D)
38 Videos
- CHEMICAL CHANGES AND REACTIONSBOOK - ICSECHAPTER - CHEMICAL CHANGES AND REACTIONSEXERCISE - EXERCISE 2(C)
30 Videos
Similar Questions
24 12Mgand26 12Mg are symbols of two isotopes of magnesium.
Compare the atoms of these isotopes with respect to :
(i) the composition of their nuclei.
(ii) their electronic configurations.
View SolutionGive reasons
35 17CIand37 17CI do not differ in their chemical reactions.
View SolutionWhy do 35 17CIand37 17CI have the same chemical properties? In what respect do these atoms differ?
View SolutionFrom the symbol 24 12Mg, state the mass number, the atomic number and electronic configuration of magnesium.
View SolutionThe ubiquitous AM-GM inequality has many
applications. It almost crops up in unlikely situations and
the solutions using AM-GM are truly elegant . Recall
that for n positive reals aiI=1,2…,n, the AM-GM inequality tells
∑1nain≥(n∏1ai)1n
The special in which the inequality turns into equality
help solves many problems where at first we seem to
have not informantion to arrive at the answer .
The number of ordered pairs (x,y) pf real numbers
satisfying the equation x8+6=8|xy|−y8 is
View SolutionThe ubiquitous AM-GM inequality has many
applications. It almost crops up in unlikely situations and
the solutions using AM-GM are truly elegant . Recall
that for n positive reals aiI=1,2…,n, the AM-GM inequality tells
∑1nain≥(n∏1ai)1n
The special in which the inequality turns into equality
help solves many problems where at first we seem to
have not informantion to arrive at the answer .
If the equation x4−4x3+ax2+bx+1=0 has
four positive roots , then the value of |a|+|b|a+b is
View SolutionThe ubiquitous AM-GM inequality has many
applications. It almost crops up in unlikely situations and
the solutions using AM-GM are truly elegant . Recall
that for n positive reals aiI=1,2…,n, the AM-GM inequality tells
∑1nain≥(n∏1ai)1n
The special in which the inequality turns into equality
help solves many problems where at first we seem to
have not informantion to arrive at the answer .
If a,b,c are positive integers satisfying
ab+c+bc+a+ca+b=32, then the value of
abc+1abc
View SolutionXMg−−→etherYDry CO2−−−−−→H+Zhot KMnO4−−−−−−−→P
The two isomeric compounds which will give the same tricarboxylic acid after the above sequence of reactions, are :
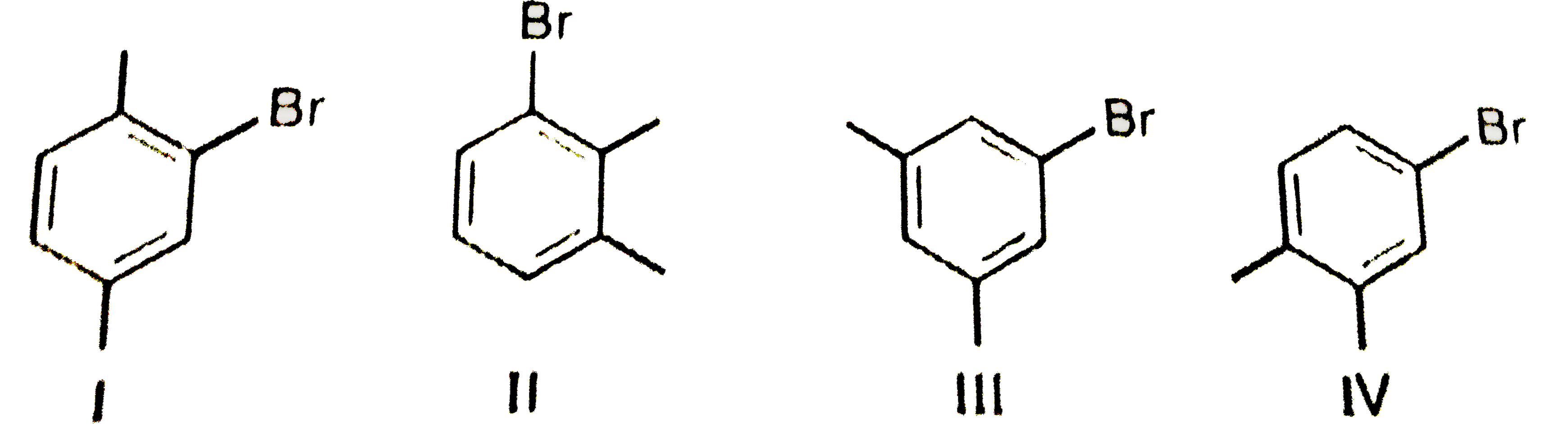
View SolutionCalcualte the number of moles of magnesium present in a magnesium ribbon weighting 12g. Molar atomic mass of magnesium is 24 g mol−1.
View SolutionFrom the symbol 42He for the element helium, write down! the mass number and the atomic number of the element.
View Solution
