The activation energy for a reaction when the temperature is raised fr

The rate of a reaction increases by 2.5 times when the temperature is raised from 300K to 310K. If K is the rate constant at 310 K will be equal to
AK
B2K
C2.5K
D3K
The activation energy for a reaction that doubles the rate when the temperature is raised from 300 K to 310 K is (log 2 = 0.3)
A $50.6 k J m o l^{- 1}$
B $75.45 k J m o l^{- 1}$
C $45.5 k J m o l^{- 1}$
D $53.4 k J m o l^{- 1}$
When the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes $K$ as a function of temperature, i.e.
$k = A e_{a}^{- E_{a} / R T}$
where
$k =$ rate constant
$A =$ a constant (frequency factor)
$E_{a} =$ energy of activation
${log}_{10} k = {log}_{10} A - \frac{E_{a}}{2.303 R} [\frac{1}{R}]$
$Y = C + M X$
It is the equation of straight line with negative slope. On plotting ${log}_{10} k$ against $[\frac{1}{T}]$ we get a straight line as shown below :

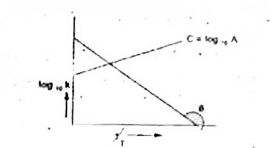
The slope gives activation energy and intercept gives frequency factor.
Also $log . \frac{k_{2}}{k_{1}} = \frac{E_{a}}{2.303} [\frac{T_{2} - T_{1}}{T_{1} T_{2}}]$
The rate of certain reaction increases by $2.5$ times when the temperature is raised from $300 K$ to $310 K$ . If $k$ is the rate constant at $300 K$ then rate constant at $310 K$ will be equal to
A $k$
B $2 k$
C $2.5 k$
D $13 k$

The activation energy for a reaction when the temperature is raised from 300K to 310K is