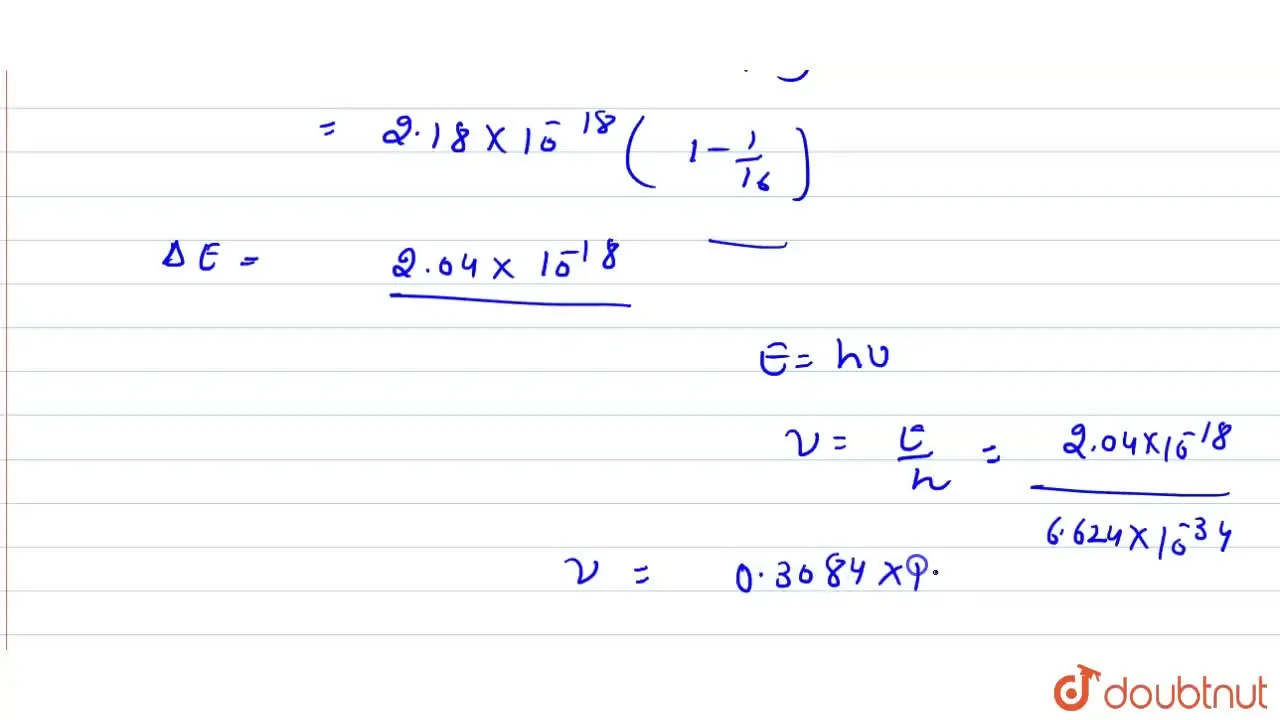The frequency of radiations emitted when electron falls from n=4 to n=1 in H−atom would be (Given E1 for H=2.18×10−18Jatom−1 and h=6.625×10−34Js.)
1.54×1015s−1
1.03×1015s−1
3.08×1015s−1
2.0×1015s−1
The correct Answer is:C
According to Bohr,s theory,
ΔE=Z2E1⎛⎝1n2f−1n2i⎞⎠
where Z2E1=− Ionization enegry
Since ΔE=hv,
we have v=ΔEh=Z2E1h⎛⎝1n2f−1n2i⎞⎠
v=2.18×10−18J6.625×10−34Js(112−142)
=0.329×1016s−1(1516)
=3.08×1015s−1
Note that we use positive sign of enegry because v has to be positive.
Related Playlists
Similar Questions
The frequency of radiations , emitted when the electron falls , from n=4 to n=1 in a hydrogen , atom
View SolutionThe frequency of radiation emiited when the electron falls n =4 to n=1 in a hydrogen atom will be ( given ionization energy of H=2.18×10−18Jatom −1andh=6.625×10−34Js)
View SolutionThe frequency of the radiation emitted when the electron falls from n = 4 to n = 1 in a hydrogen atom will be
(Given ionization energy of H=2.18×10−18 J atom−1 and h=6.625×10−34 Js)View SolutionThe frequency of radiation emiited when the electron falls n =4 to n=1 in a hydrogen atom will be ( given ionization energy of H=2.18×10−18Jatom −1andh=6.625×10−34Js)
View SolutionThe frequency of radiation emiited when the electron falls n =4 to n=1 in a hydrogen atom will be ( given ionization energy of H=2.18×10−18Jatom −1andh=6.625×10−34Js)
View SolutionThe wavelength of the radiation emitted when an electron falls from Bohr 's orbit 4 to 2 in H atom is
View SolutionCalculate the wavelength and energy for radiation emitted for the electron transition from infinite (∞) to stationary state of the hydrogen atom
R=1.0967×107m−1,h=6.6256×10−34Js and c=2.979×108ms−1View SolutionThe wavelength of the radiation emitted , when in a hydrogen atom electron falls from infinity to stationary state 1 , would be :
(Rydberg constant = 1.097×107m−1)View SolutionThe recoil speed of hydrogen atom after it emits a photon in going from n=2state→n=1 state is nearly [TakeR∞=1.1×107mandh=6.63×10−34Js]
View SolutionThe kinetic energy of the electron emitted when light of frequency 3.5×1015Hz falls on a metal surface having threshold frequency 1.5×1015Hz is (h=6.6×10−34Js).
View Solution