The relation between pressure exerted by an ideal gas and observed pressure is given by the equation
(i) If pressure is taken in , number of moles in mol and volume in , Calculate the unit of .a..
(ii) What will be the unit of .a. when pressure is in atmosphere and volume in ? Solution in Gujrati
Given that,
(i) a = If units of ,
units of , units of n = mol
then, units of
(ii) If units of p = atm, units of , units of n = mol
then, units of
= atm
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - STATES OF MATTER EXERCISE - SECTION - D SOLUTION OF NCERT EXEMPLAR PROBLEMS (Matching The Columns)3videos
STATES OF MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - STATES OF MATTER EXERCISE - SECTION - D SOLUTION OF NCERT EXEMPLAR PROBLEMS (Assertion and Reason)6videos
STATES OF MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - STATES OF MATTER EXERCISE - SECTION - D SOLUTION OF NCERT EXEMPLAR PROBLEMS (Multiple Choice Questions)17videos
STATES OF MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - Section - D (Solutions of NCERT Exemplar Problems) (Long Answer Type Questions)4videos
SOME BASIC CONCEPTS OF CHEMISTRY
- BOOK - KUMAR PRAKASHANCHAPTER - STRUCTURE OF ATOMEXERCISE - QUESTINS PAPER FROM MODULE (SECTION -D)2videos
STRUCTURE OF ATOM
Similar Questions
Match the graphs between the following variables with their names :
 03:50View Solution
03:50View SolutionAssertion (A) : Three states of matter are the result of balance between intermolecular forces and thermal energy of the molecules.
Reason (R ) : Intermolecular forces tend to keep the molecules together but thermal energy of molecules tends to keep them apart.02:24View SolutionA person living in Shimla observed that cooking food without using pressure cooker takes more time. The reason for this observation is that at high altitude :
02:51View SolutionA vessel contains 1.6 g of dioxygen at STP (273.15 K, 1 atm pressure). The gas is now transferred to another vessel at constant temperature, where pressure becomes half of the original pressure. Calculate
(A) volume of the new vessel.
(B) number of molecules of dioxygen.05:06View SolutionExplain Heisenberg’s uncertainty principle.
02:59View SolutionIf n moles of an ideal gas are expanded is isothermally and reversibly from an initial state in which it has pressure p1 and volume V1 to the final state of volume V2 and pressure P2, then
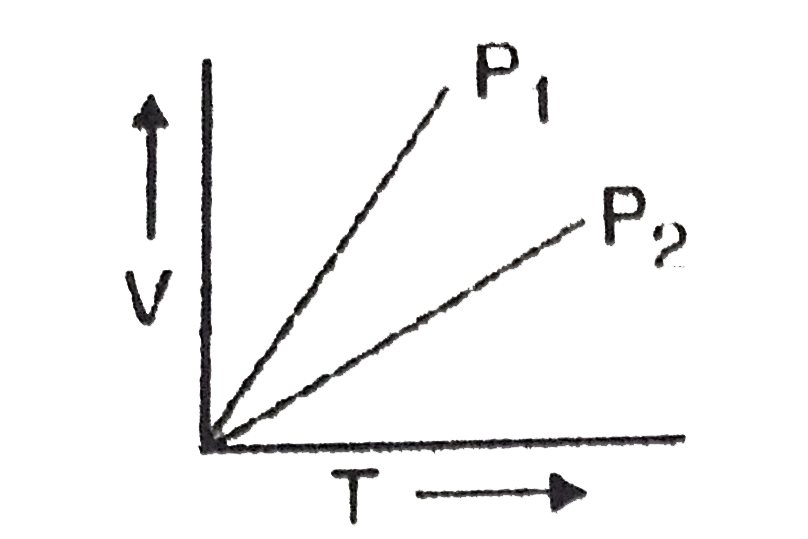
03:57View SolutionV vs T curves at constant pressure P1 and P2 for an ideal gas are shown below
Which is correct ?View Solutionvan der Waal's equation for calculating the pressure of a non ideal gas is
(P+an2V2)(V−nb)=nRT
van der Waal's suggested that the pressure exerted by an ideal gas , Pideal, is related to the experiventally measured pressure, Pideal by the equation
Pideal=Preal↑observed pressure+an2V2↑currection term
Constant 'a' is measure of intermolecular interaction between gaseous molecules that gives rise to nonideal behavior. It depends upon how frequently any two molecules approach each other closely. Another correction concerns the volume occupied by the gas molecules. In the ideal gas equation, V represents the volume of the container. However, each molecule does occupy a finite, although small, intrinsic volume, so the effective volume of the gas vecomes (V-nb), where n is the number of moles of the gas and b is a constant. The term nb represents the volume occupied by gas particles present in n moles of the gas .
Having taken into account the corrections for pressure and volume, we can rewrite the ideal gas equation as follows :
(P+an2V2)corrected pressure(V−nb)corrected volume=nRT
For non-zero value of force of attraction between gas moleculer at large volume, gas equation will be :03:49View SolutionThe relation between pressure exerted by an ideal gas (pideal) and observed pressure (preal) is given by the equation,
pideal=preal+an2V2
(i) If pressure is taken in NM−2, number of moles in mol and volume in m3, calculate the unit of 'a'.
(ii) What will be the unit of 'a' when pressure is in atmosphere and volume in dm3?02:06View SolutionThe relation between pressure exerted by an ideal gas (p_("ideal")) and observed pressure (p_("real")) is given by the equation " " p_("ideal")=p_("real")+(an^(2))/(V^(2)) If pressure is taken in N m^(-2) , number of moles in mol and volume in m^(3) , calculate the unit of 'a'. What will be the unit of 'a' when pressure is in atmosphere is in atmosphere and volume in dm^(3) ?
01:56View Solutionएक आदर्श गैस का प्रारम्भिक आयतन V1 तथा दाब P1=6 वायुमण्डलीय दाब है। समतापी प्रसार द्वारा इसका आयतन V2 तथा दाब P2=3 वायुमण्डलीय हो जाता है। तत्पश्चात रूद्धोष्म प्रसार द्वारा इसका आयतन V3 तथा दाब P3=2 वायुमण्डलीय दाब हो जाता है। दाब-आयतन परिवर्तन का कच्चा आरेख (rough sketch) खींचिए V2/V1 तथा V3/V2 के मान प्राप्त कीजिए ।
View SolutionWhich of the following statement is correct?
(i) Real gases show deviations from ideal gas law because molecules interact with each other.
(ii) Due to interaction of molecules the pressure exerted by the gas is given as:
preal=pideal+an2V2
(iii) Value of 'a' is measure of magnitude of intermolecular attractive forces within the gas and depends on temperature and pressure of gas.
(iv) At high pressure volume occupied instead of moving in volume V, these are not restricted to volume (V-nb)View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and final pressure P_(I) . The same gas is expanded adiabatically to a volume 2V and final pressure in this case is P_(A) . In terms of the ratio of the two specific heats for the gas gamma , the ratio P_(I)//P_(A) is
02:45View SolutionThe relation between pressure exerted by an ideal gas (pideal) and observed pressure (preal) is given by the equation, p_("ideal") = p_("real") + (an^(2))/(V^(2)) If pressure is taken in Nm^(-2) , number of moles in mol and volume in m_(3) , calculate the unit of ' a '.
05:43View SolutionThe relation between pressure exerted by an ideal gas (pideal) and observed pressure (preal) is given by the equation,
pideal=preal+an2V2
What will be the unit of ' a ' when pressure is in atmosphere and volume in dm3 ?02:20View Solution

