A ball falls freely form a height onto and smooth inclined plane forming an angle a with the horizontal. Find the ratio of the distance between the points at which the jumping ball strikes the inclined plane. Assume the impacts to be elastic.
The correct Answer is:1:2:3
Let v0 the velocity with which it strikes the plane.
ax=gsina, ay=−gcosa
Component of velocity along the plane is v0sinα and component perenducilar to plane isv0cosα. Collision is elastic hence v0sinα remains uchanged while v0cosα reverses its direcions.
When it stirkes at B, its component perpendicular to plane i.e., v0cosα and hence the time of flight T for each collision remains unchanged while component parallel to pane becomes
v0sinα+(gsinα)T

{vx=ux+axt}
Here T=2v0cosαgcosα=2v0g
and R1=AB=s−x=uxT+12axT2
=(v0sinα)2v0g+12(gsinα)(2v0g)2
R1=(402sinα)g
Next time
R2=sx={v0sinα.T}T+12(gsinalph)T2
substituting the values
R2{v0sina+gsinα.2v0g}{2v0v}+12(gsinα)(2v0g)2
=8v20sinαg
Similarly we can show that R3=(12v20sinα)g
or R1:R2:R3=1:2:3
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A ball starts falling with zero initial velocity on a smooth inclined plane forming an angle α with the horizontal. Having fallen the distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time?
View SolutionA ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle α with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane. At what distance from the impact point will the ball rebound for the second time ?
View Solution
Knowledge Check
A ball starts falling freely from a height h from a point on the inclined plane forming an angle α with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at
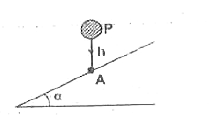 At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
At=√8hg after it strikes the inclined at ABt=√2hgafter it strikes the inclined at A.Ca distance 4h sin α from A along the inclineDa distance 8h sin α from A along the incline
A ball starts falling with zero initial velocity on to a smooth inclined plane forming an angle α with the horizontal. Having fallen a distance h, the ball rebounds elastically off the inclined plane . At what distance from the impact point will the ball rebound for the second time ?
View SolutionA ball starts falling freely from a height h from a point on the inclined plane forming an angle α with the horizontal as shown. After collision with the incline it rebounds elastically off the plane. Then it again strikes the incline at
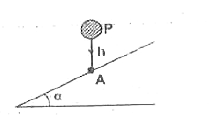
View SolutionA block is placed on a smooth inclined plane at an angle 'θ' to the horizontal. The acceleration must the plane be moved horizontally so that the block to fall freely is
View SolutionA uniform solid cylinder of radius R=15cm rolls over a horizontal plane passing into an inclined plane forming an angle α=30∘ with the horizontal(figure). Find the maximum value of the velocity v0 which still permits the cylinder to roll onto the inclined plane section without a jump. The sliding is assumed to be absent.

View SolutionA ball is projected from the foot of an inclined plane of inclination 30∘ at an angle 60∘ with the horizontal,with velocity 20√3ms−1 .The time after which the ball will strike the plane is
View SolutionA ball is projected form a point A on a smooth inclined plane which makes an angle a to the horizontal. The velocity of projection makes an angle θ with the plane upwards. If on the second bounce the ball is moving perpendicular to the plane, find e in terms of α and θ. Here e is the coefficient of restitution between the ball and the plane.
View SolutionA ball is projected form a point A on a smooth inclined plane which makes an angle a to the horizontal. The velocity of projection makes an angle θ with the plane upwards. If on the second bounce the ball is moving perpendicular to the plane, find e in terms of α and θ. Here e is the coefficient of restitution between the ball and the plane.
View Solution
