A ball is thrown up with a certain velocity at angle θ to the horizontal. The kinetic energy varies with height h of the particle as:
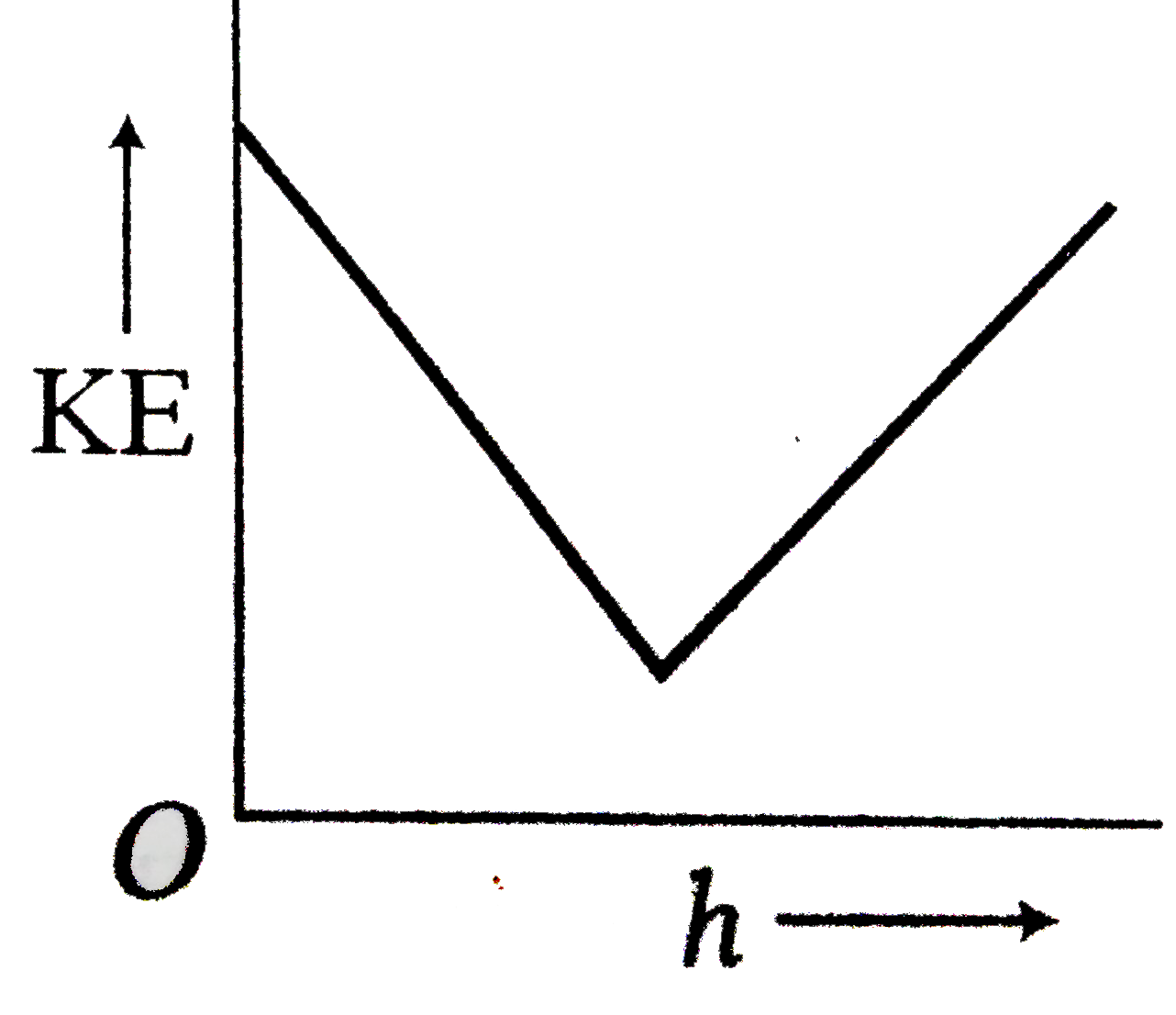
The correct Answer is:A
To solve the problem of how the kinetic energy of a ball thrown at an angle θ to the horizontal varies with height h, we can follow these steps:
Step 1: Understand the Initial Conditions
- A ball is thrown with an initial velocity v0 at an angle θ to the horizontal.
- The initial kinetic energy (KE) at the point of release (point O) is given by:
KEO=12mv20
- The potential energy (PE) at point O can be considered zero since we can take this point as our reference level.
Step 2: Apply Conservation of Energy
- According to the conservation of mechanical energy, the total mechanical energy at the initial point (O) is equal to the total mechanical energy at any point (A) at height h:
KEO+PEO=KEA+PEA
- Since PEO=0, we have:
12mv20=KEA+mgh
Step 3: Express Kinetic Energy at Height h
- Rearranging the equation gives us the kinetic energy at height h:
KEA=12mv20−mgh
Step 4: Simplify the Expression
- Factoring out m:
KEA=m(12v20−gh)
- This shows that the kinetic energy decreases linearly with increasing height h.
Step 5: Analyze the Graph
- The kinetic energy is maximum at the ground (when h=0) and decreases as the height increases.
- At the maximum height hmax, the kinetic energy will not be zero because the ball still has horizontal velocity v0cosθ. Thus, the kinetic energy at the highest point can be calculated as:
KEmax=12m(v0cosθ)2
- The graph of kinetic energy (KE) versus height (h) will be a straight line with a negative slope, indicating that as height increases, kinetic energy decreases.
Final Graph Representation
- The graph starts from KE=12mv20 at h=0 and decreases linearly, approaching a value that corresponds to the kinetic energy at the maximum height.
Summary
- The kinetic energy of the ball decreases linearly with height h until it reaches its maximum height, where it retains some kinetic energy due to horizontal motion.
- A ball is thrown with an initial velocity v0 at an angle θ to the horizontal.
- The initial kinetic energy (KE) at the point of release (point O) is given by:
KEO=12mv20
- The potential energy (PE) at point O can be considered zero since we can take this point as our reference level.
- According to the conservation of mechanical energy, the total mechanical energy at the initial point (O) is equal to the total mechanical energy at any point (A) at height h:
KEO+PEO=KEA+PEA
- Since PEO=0, we have:
12mv20=KEA+mgh
- Rearranging the equation gives us the kinetic energy at height h:
KEA=12mv20−mgh
- Factoring out m:
KEA=m(12v20−gh)
- This shows that the kinetic energy decreases linearly with increasing height h.
- The kinetic energy is maximum at the ground (when h=0) and decreases as the height increases.
- At the maximum height hmax, the kinetic energy will not be zero because the ball still has horizontal velocity v0cosθ. Thus, the kinetic energy at the highest point can be calculated as:
KEmax=12m(v0cosθ)2
- The graph of kinetic energy (KE) versus height (h) will be a straight line with a negative slope, indicating that as height increases, kinetic energy decreases.
- The graph starts from KE=12mv20 at h=0 and decreases linearly, approaching a value that corresponds to the kinetic energy at the maximum height.
- The kinetic energy of the ball decreases linearly with height h until it reaches its maximum height, where it retains some kinetic energy due to horizontal motion.
Topper's Solved these Questions
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - B. Medical entrance
1 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrance
12 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - A. Taking it together
1 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
Similar Questions
A ball is thrown up with a certain velocity at anangle θ to the horizontal. The kinetic energy KE of the ball varies with horizontal displacements as:
View SolutionA body is projected horizontally with a velocity of ums−1 at an angle θ with the horizontal. The kinetic energy at intial the highest point is 34th of the kinetic energy. The value of θ is :
View Solution
Knowledge Check
A particle is thrown with a speed is at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal, its speed changes to v, then
Av=v0cosθBv=v0cosθ⋅cosϕCv=v0cosθ⋅secϕDv=v0secθ⋅cosϕ
A projectile is thrown with velocity v at an angle θ with the horizontal. When the projectile is at a height equal to half of the maximum height,.
The vertical component of the velocity of projectile is.
View SolutionA projectile is thrown with velocity v at an angle θ with the horizontal. When the projectile is at a height equal to half of the maximum height,.
The velocity of the projectile when it is at a height equal to half of the maximum height is.
View SolutionA particle is projected at an angle θ from the horizontal with kinetic energy (T). What is the kinetic energy of the particle at the highest point ?
View SolutionA cricket ball is hit for a six the bat at an angle of 45∘ to the horizontal with kinetic energy K. At the highest point, the kinetic energy of the ball is
View SolutionA cricket ball is hit for a six the bat at an angle of 45∘ to the horizontal with kinetic energy K. At the highest point, the kinetic energy of the ball is
View SolutionA particle is thrown with a speed u at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal. Its speed changes to v :
View SolutionA particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.
View Solution
