A ball of mass m1 and another ball of mass m2 are dropped from equal height. If the time taken by the balls are t1 and t2, respectively, then
t1=t2
t1=2t2
t1t2=m1m2
t1t2=m2m1
The correct Answer is:A
To solve the problem, we need to analyze the motion of two balls dropped from the same height. We will use the equations of motion to derive the relationship between the times taken by the two balls.
1. Identify the Given Information:
- Two balls with masses m1 and m2 are dropped from the same height h.
- The time taken by ball 1 is t1 and by ball 2 is t2.
- Both balls are dropped from rest, so their initial velocities u=0.
2. Use the Equation of Motion:
- The equation of motion for an object in free fall is given by:
s=ut+12at2
- Here, s is the displacement (height h), u is the initial velocity (which is 0), a is the acceleration (which is g, the acceleration due to gravity), and t is the time taken.
3. Apply the Equation for Both Balls:
- For ball 1:
h=0⋅t1+12gt21⟹h=12gt21
- For ball 2:
h=0⋅t2+12gt22⟹h=12gt22
4. Set the Equations Equal to Each Other:
- Since both balls are dropped from the same height h, we can set the two equations equal:
12gt21=12gt22
5. Simplify the Equation:
- We can cancel 12g from both sides (assuming g≠0):
t21=t22
6. Take the Square Root:
- Taking the square root of both sides gives:
t1=t2
Conclusion:
The time taken by both balls to reach the ground is the same, regardless of their masses. Therefore, the relationship is:
t1=t2
- Two balls with masses m1 and m2 are dropped from the same height h.
- The time taken by ball 1 is t1 and by ball 2 is t2.
- Both balls are dropped from rest, so their initial velocities u=0.
- The equation of motion for an object in free fall is given by:
s=ut+12at2
- Here, s is the displacement (height h), u is the initial velocity (which is 0), a is the acceleration (which is g, the acceleration due to gravity), and t is the time taken.
- For ball 1:
h=0⋅t1+12gt21⟹h=12gt21
- For ball 2:
h=0⋅t2+12gt22⟹h=12gt22
- Since both balls are dropped from the same height h, we can set the two equations equal:
12gt21=12gt22
- We can cancel 12g from both sides (assuming g≠0):
t21=t22
- Taking the square root of both sides gives:
t1=t2
The time taken by both balls to reach the ground is the same, regardless of their masses. Therefore, the relationship is:
t1=t2
Topper's Solved these Questions
Similar Questions
A ball of mass 1 kg is dropped from a height of 5 m. What is its speed at this instant ?
View SolutionA ball is dropped from a balloon rising up with a velocity of 50 m/s. When the ball is dropped the balloon was at a height of 100 m. Find the time taken by the ball to reach the ground.
View Solution
Knowledge Check
- Question 1 - Select One or More
A ball of mass m1, collides elastically and head on with ball of mass m2 at rest. Then
AThe transfer of kinetic energy to the second ball is maximum when m1=m2BThe change of momentum of first ball is maximum, when m1<<m2.CThe velocity of the second ball is maximum, when m1>>m2.DNone of these - Question 2 - Select One
A ball is dropped from a height of 10 m, as it falls,
Aits velocity increases and acceleration decreases.Bits velocity decreases and acceleration increases.Cits velocity increases and acceleration remains constant.Dits velocity and acceleration remains constant. - Question 3 - Select One
Two balls are dropped from heights h and 2h respectively. The ratio of time taken by these balls to reach the earth is
A1:√2B√2:1C2:1D1:4
Body A of mass M is dropped from a height of 1 m and body. B of mass 3M is dropped from a height of 9 m. The ratio of time taken by the bodies 1 and 2 to reach the ground is
View SolutionIn the figure shown, the heacvy ball of mass 2m rests on the horizontal surface and the lighter balls of mass m is dropped from a height h>2l. At the instant the string gets taut, the upward velocity of the heavy ball will be :
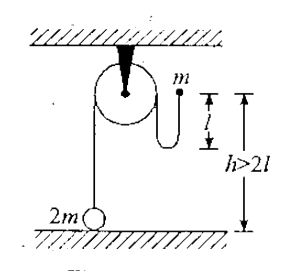 View Solution
View SolutionIn the figure shown, the heavy ball of mass 2m, rests on the horizontal surface and the lighter ball of mass m is dropped from a height h>2l. At the instant the string gets taut, the upward the velocity of the heavy ball will be
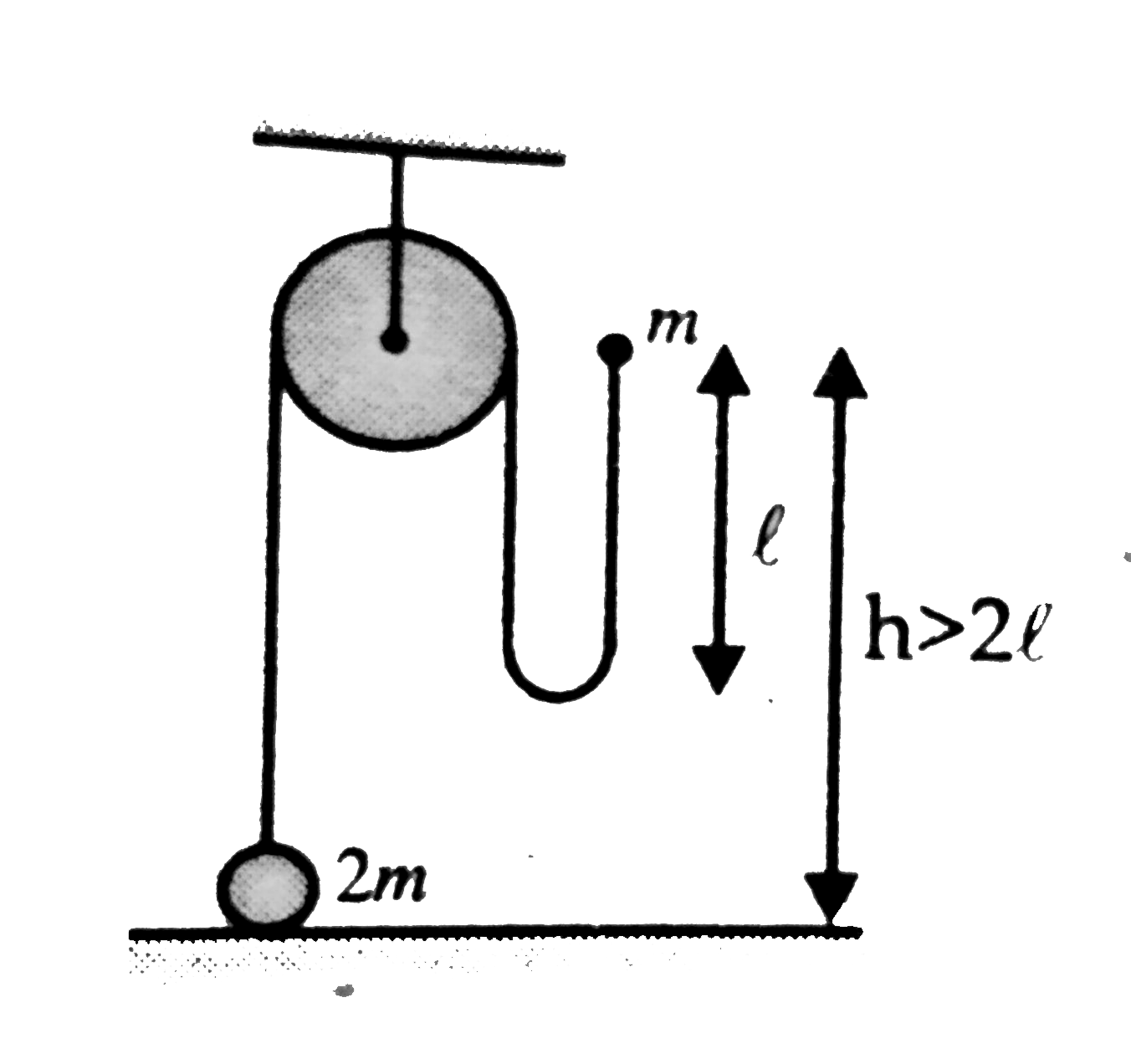 View Solution
View SolutionA ball of mass m1 moving with a certain speed collides elastically with another ball of mass m2 kept at rest . If the first ball starts moving in reversed direction after the impact then
View SolutionA spherical ball of mass m1 colliddes head on with another ball of mass m2 at rest . The collision is elastic . The fraction of kintic energy lost by m1 is :
View Solution

