A battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
To find the current flowing through the battery, we can follow these steps:
Step 1: Identify the given values
- EMF of the battery (E) = 2 V
- Internal resistance of the battery (r) = 0.5 Ω
- External resistance (R) = 1.5 Ω
Step 2: Calculate the total resistance in the circuit
Since the internal resistance and the external resistance are in series, the total resistance (R_total) can be calculated as:
Rtotal=R+r
Substituting the values:
Rtotal=1.5Ω+0.5Ω=2Ω
Step 3: Apply Ohm's Law to find the current
Ohm's Law states that the current (I) can be calculated using the formula:
I=ERtotal
Substituting the values:
I=2V2Ω=1A
Conclusion
The current flowing through the battery is 1 ampere.
---
- EMF of the battery (E) = 2 V
- Internal resistance of the battery (r) = 0.5 Ω
- External resistance (R) = 1.5 Ω
Since the internal resistance and the external resistance are in series, the total resistance (R_total) can be calculated as:
Rtotal=R+r
Substituting the values:
Rtotal=1.5Ω+0.5Ω=2Ω
Ohm's Law states that the current (I) can be calculated using the formula:
I=ERtotal
Substituting the values:
I=2V2Ω=1A
The current flowing through the battery is 1 ampere.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Objective 1
15 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
A battery of e.m.f. 10V and internal resistance 0.5ohm is connected across a variable resistance R. The value of R for which the power delivered in it is maximum is given by
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistors ? What is the terminal voltage of the battery when the circuit is closed ?
View Solution
Knowledge Check
A battery of emf 15 V and internal resistance of 4Ω is connected to a resistor. If the current in the circuit is 2A and the circuit is closed. Resistance of the resistor and terminal voltage of the battery will be
A2.5Ω,6VB3.5Ω,6VC2.5Ω,7VD3.5Ω,7VA battery having 12V emf and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 1A, then the resistance of resistor and lost voltage of the battery when circuit is closed will be
A7Ω,7VB8Ω,8VC9Ω,9VD9Ω,10V
Three equal resistances, each of RΩ are connected as shown in figure. A battery of emf 2 V and internal resistance 0.1Ω is connected across the circuit. Calculate the value of R for which the heat generated in the circuit is maximum?
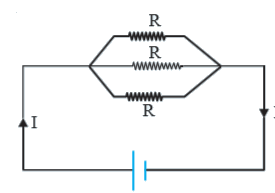
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
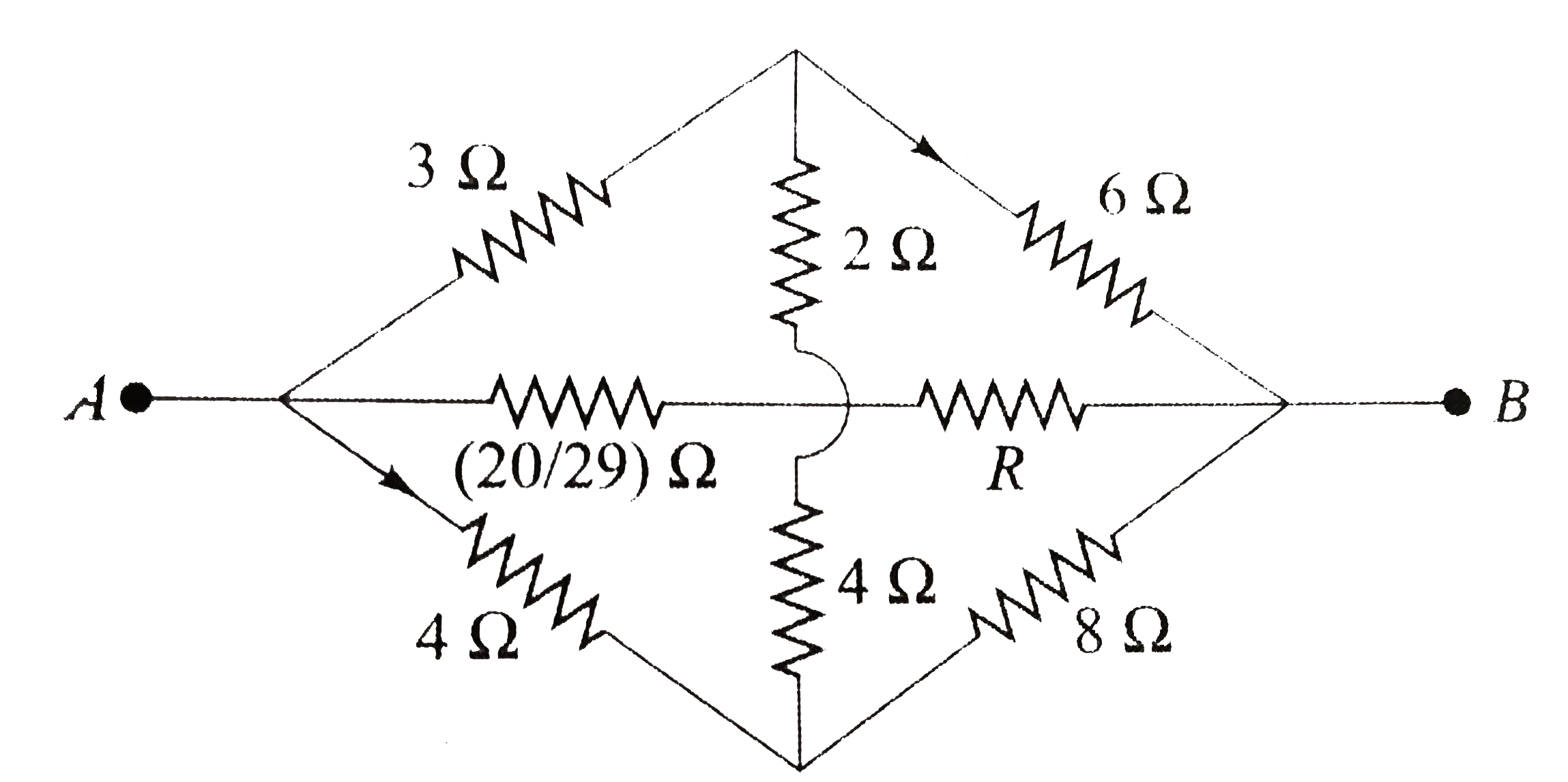 .
.
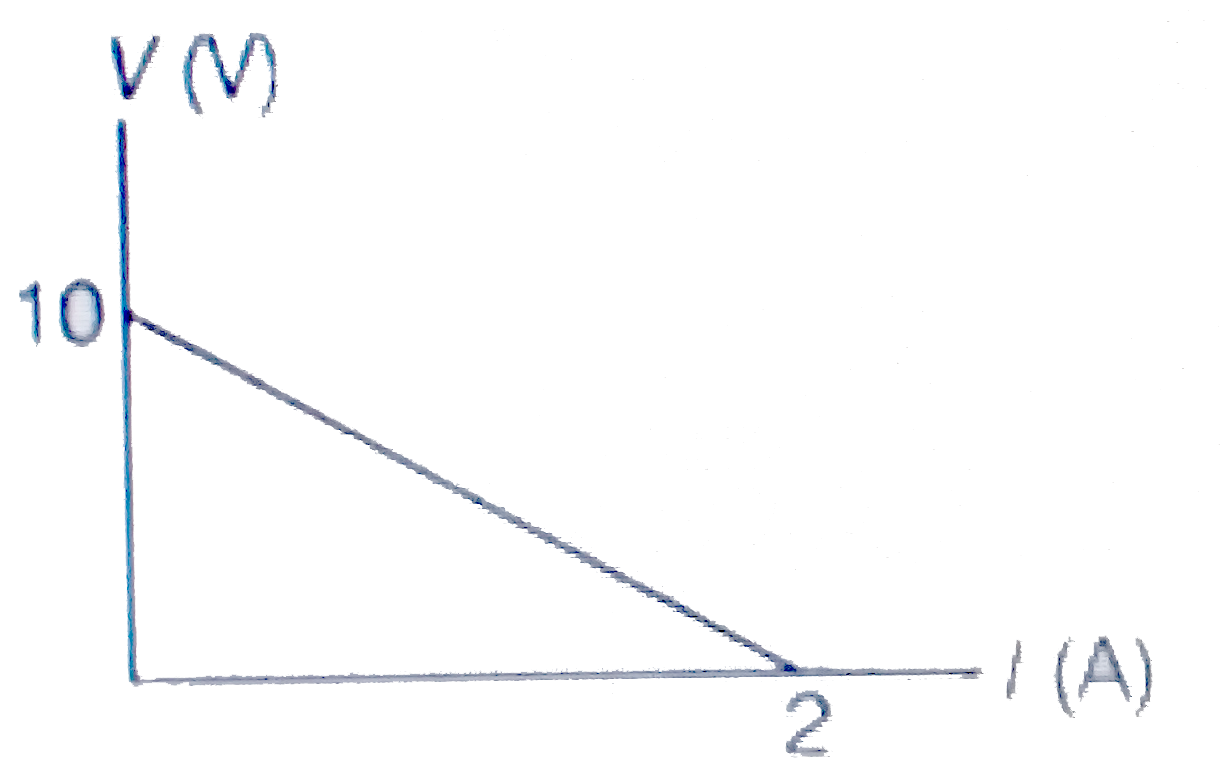
View SolutionA battery of emf E and internal resistance r is connected across a resistance R. Resistance R can be adjusted to any value greater than or equal to zero. A graph is plotted between the current passing through the resistance (I) and potential difference across the termainals of the battery (V). Maximum power developed across the resistance R is
View SolutionThe potential difference between the terminals of a battery of emf 6.0V and internal resistance1(Ω)drops to 5.8 V when connected across an external resistor. Find the resistance of the external resistor.
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionA battery of emf 2.0 V and internal resistance 0.50(Ω)supplies a current of 100 mA. Find (a) the potential defference across the terminals of the battary and (b) the thermal energy develop in the battery in 10 s.
View Solution
