A battery of unknown emf and internal resistance is given to a student for the experiment. When student connects the battery to an external resistance of 10Ω then 1A current flows through the circuit and when the same is connected to 15Ω resistance then 0.75 A current flows through the circuit . Calculate the emf and internal resistance of the given battery.
To solve the problem, we need to use the information provided about the current flowing through the circuit with different external resistances. We can derive two equations based on Ohm's law and the concept of internal resistance.
1. Understanding the Circuit:
- When the battery is connected to an external resistance R1=10Ω, the current I1=1A flows through the circuit.
- When the battery is connected to an external resistance R2=15Ω, the current I2=0.75A flows through the circuit.
2. Applying Ohm's Law:
- The total voltage (emf) of the battery E can be expressed in terms of the internal resistance r and the external resistance R using Ohm's law:
E=I(R+r)
3. Setting Up the Equations:
- For the first case with R1=10Ω:
E=I1(R1+r)⟹E=1(10+r)⟹E=10+r(Equation 1)
- For the second case with R2=15Ω:
E=I2(R2+r)⟹E=0.75(15+r)⟹E=11.25+0.75r(Equation 2)
4. Equating the Two Expressions for E:
- From Equation 1 and Equation 2, we can set them equal to each other:
10+r=11.25+0.75r
5. Solving for r:
- Rearranging the equation:
10+r−0.75r=11.25
10+0.25r=11.25
0.25r=11.25−10
0.25r=1.25
r=1.250.25=5Ω
6. Finding E:
- Now substitute r back into Equation 1 to find E:
E=10+r=10+5=15V
Final Results:
- The emf of the battery E=15V
- The internal resistance of the battery r=5Ω
- When the battery is connected to an external resistance R1=10Ω, the current I1=1A flows through the circuit.
- When the battery is connected to an external resistance R2=15Ω, the current I2=0.75A flows through the circuit.
- The total voltage (emf) of the battery E can be expressed in terms of the internal resistance r and the external resistance R using Ohm's law:
E=I(R+r)
- For the first case with R1=10Ω:
E=I1(R1+r)⟹E=1(10+r)⟹E=10+r(Equation 1)
E=I2(R2+r)⟹E=0.75(15+r)⟹E=11.25+0.75r(Equation 2)
- From Equation 1 and Equation 2, we can set them equal to each other:
10+r=11.25+0.75r
- Rearranging the equation:
10+r−0.75r=11.25
10+0.25r=11.25
0.25r=11.25−10
0.25r=1.25
r=1.250.25=5Ω
- Now substitute r back into Equation 1 to find E:
E=10+r=10+5=15V
- The emf of the battery E=15V
- The internal resistance of the battery r=5Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE PROBLEMS
71 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
When a celll is connected to an external resistance R1, current through it is i1. When the same cell is connected to an external resistance R2, current through it is i2. Calculate the emf and internal resisance of the cell.
View SolutionA battery supplies a current of 0.9 A through a 2Ω resistor and a current of 0.3 A through a 7Ω resistor. Calculate the emf and internal resistance of the battery.
View Solution
Knowledge Check
A series combination of two resistors 1Ω each is connected to a 12 V battery of internal resistance 0.4Ω. The current flowing through it will be
A3.5AB5AC6AD10AA battery has e.m.f. 4 V and internal resistance r . When this battery is connected to an external resistance of 2 ohms , a current of 1 amp . flows in the circuit. How much current will flow if the terminals of the battery are connected directly
A4 and 2B2 and 4C4 and 4D2 and 2
A resistance of 1Ω is connected to a battery of emf 2 V and internal resistance 0.4Ω what current is flowing through the circuit ? If another battery of double the emf is connected in series with the earlier one then current flowing in the circuit becomes double . what should be the internal resistance of battery ?
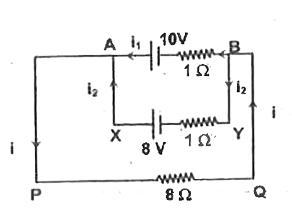
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
View SolutionA wire of resistance 4Ω is connected to a battery having an internal resistance of 1Ω For a current of 6 A to flow through the circuit what should be the emf of the battery ?
View SolutionA battery of e.m.f 10V and internal resistance 3Omega is connected to a resistor.If the current in the circuit is 0.5A,then the resistance of the resistor is
View SolutionA bulb of resistance 5Ω is connected to a battery of emf 4.2 V and internal resistance 1Ω. Find the current through the bulb.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View Solution
