A bird in air looks at a fish directly below it inside in a transparent liquid in a tank. If the distance of the fish as estimated by the bird is h1 and that of the bird as estimated by the fish is h2, then the refractive index of the liquid is
h2h1
h1h2
h1+h2h1−h2
h1−h2h1+h2
The correct Answer is:A
To find the refractive index of the liquid in which the fish is located, we can analyze the situation using the distances observed by both the bird and the fish. Let's denote the refractive index of the liquid as μ, the distance of the fish as estimated by the bird as h1, and the distance of the bird as estimated by the fish as h2.
1. Understanding the Setup:
- A bird in air looks down at a fish in a tank filled with a transparent liquid. The bird sees the fish at a distance h1, while the fish sees the bird at a distance h2.
- The light rays from the fish will bend when they pass from the liquid to the air, and the light rays from the bird will bend when they pass from air to the liquid.
2. Applying Snell's Law:
- When light travels from one medium to another, Snell's Law states that:
n1sin(θ1)=n2sin(θ2)
- Here, n1 is the refractive index of air (approximately 1), and n2 is the refractive index of the liquid (μ).
3. Distance Observed by the Bird:
- The distance h1 that the bird sees the fish can be expressed as:
h1=x+yμ
- Here, x is the distance from the surface of the liquid to the fish, and y is the distance from the bird to the surface of the liquid.
4. Distance Observed by the Fish:
- The distance h2 that the fish sees the bird can be expressed as:
h2=μ(x+y)
5. Setting Up the Equations:
- We have two equations:
1. h1=x+yμ (Equation 1)
2. h2=μ(x+y) (Equation 2)
6. Manipulating the Equations:
- From Equation 1, we can express y:
y=μ(h1−x)
- Substitute y into Equation 2:
h2=μ(x+μ(h1−x))
- Simplifying gives:
h2=μ2h1+μx−μ2x
- Rearranging yields:
h2=μ2h1+x(μ−μ2)
7. Finding the Refractive Index:
- By adding the two equations after multiplying Equation 1 by μ:
μh1+h2=μx+y
- Rearranging leads to:
2μx+y=h2
- From this, we can derive:
μh1=h2
- Therefore, we can express the refractive index μ as:
μ=h2h1
Final Answer:
The refractive index of the liquid is given by:
μ=h2h1
- A bird in air looks down at a fish in a tank filled with a transparent liquid. The bird sees the fish at a distance h1, while the fish sees the bird at a distance h2.
- The light rays from the fish will bend when they pass from the liquid to the air, and the light rays from the bird will bend when they pass from air to the liquid.
- When light travels from one medium to another, Snell's Law states that:
n1sin(θ1)=n2sin(θ2)
- Here, n1 is the refractive index of air (approximately 1), and n2 is the refractive index of the liquid (μ).
- The distance h1 that the bird sees the fish can be expressed as:
h1=x+yμ
- Here, x is the distance from the surface of the liquid to the fish, and y is the distance from the bird to the surface of the liquid.
- The distance h2 that the fish sees the bird can be expressed as:
h2=μ(x+y)
- We have two equations:
1. h1=x+yμ (Equation 1)
2. h2=μ(x+y) (Equation 2)
- From Equation 1, we can express y:
y=μ(h1−x)
- Substitute y into Equation 2:
h2=μ(x+μ(h1−x))
- Simplifying gives:
h2=μ2h1+μx−μ2x
- Rearranging yields:
h2=μ2h1+x(μ−μ2)
- By adding the two equations after multiplying Equation 1 by μ:
μh1+h2=μx+y
- Rearranging leads to:
2μx+y=h2
- From this, we can derive:
μh1=h2
- Therefore, we can express the refractive index μ as:
μ=h2h1
The refractive index of the liquid is given by:
μ=h2h1
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
A fish in a lake (refractive index 4/3 for water ) is viewed through a convex lens. From water surface, the lens is placed in air at half of the distance of the fish from the water surface, so that the image is formed at the fish itself. The focal length of the lens is how many times the depth of fish in water?
View SolutionConsider the situation as shown in the diagram.
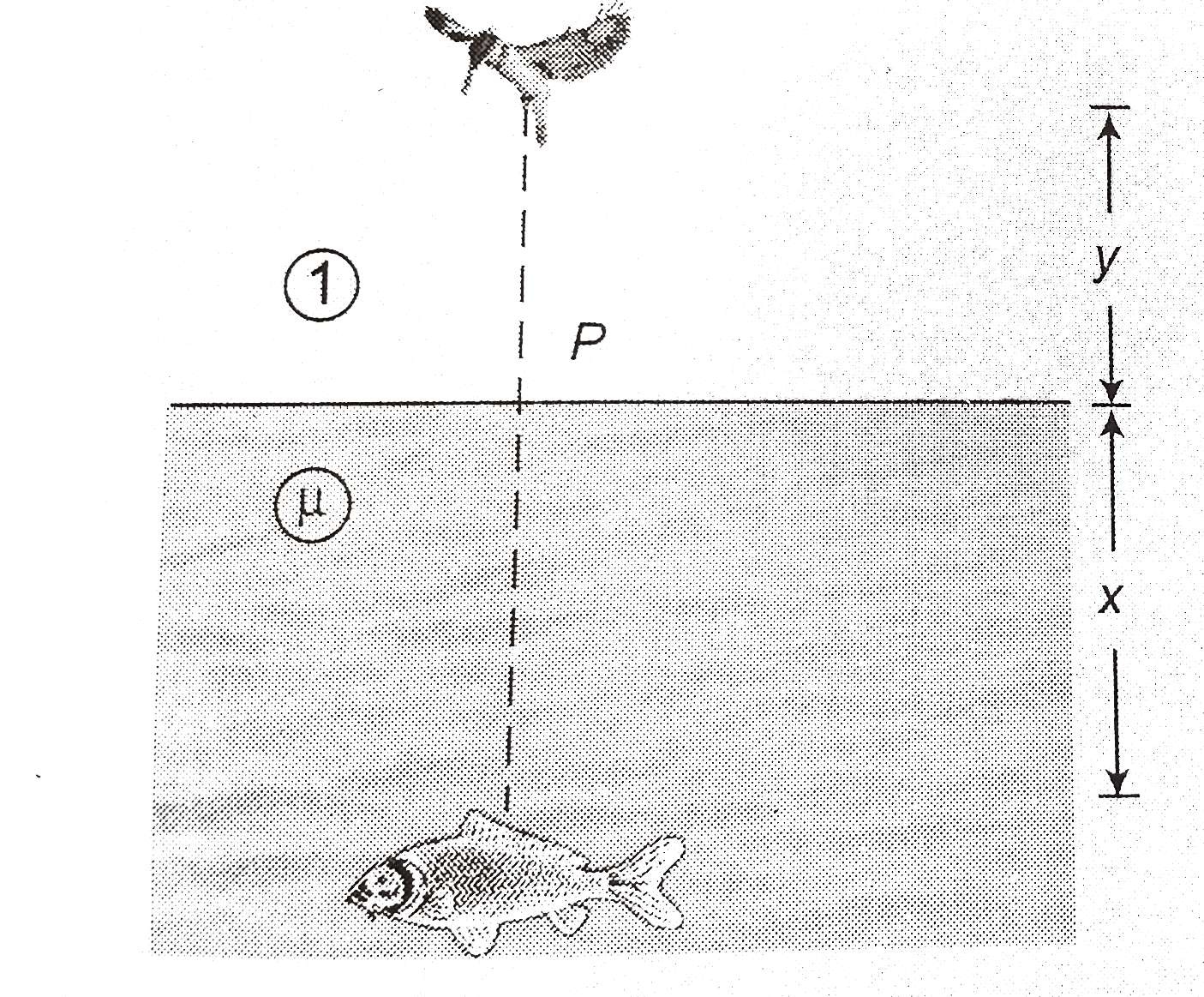
Find the distance between bird and fish as seen by (a) bird and (b) fish
View SolutionThe back wall of an aqaurium is a mirror that is 30 cm away from the fron wall. The sides to the tank are negligibly thin. A fish is swimming midway between the front and back walls.
a. An image of the fish appears behind the mirror. How far dows this image appear to be from the front wall of the aquarium?
b. Would the refractive index of the liquid have to be larger or smaller in order for the image of the fish to appear in front of the mirror, rather than behind it? Find the limiting value of this refractive index. Initially, water is there in aquarium having refractive index 4/3
View SolutionA rectangular tank filled with some liquid is accelerated along a horizontal surface at 403ms−2. Inside the liquid, a laser pointer is fixed a the centre of the tank which shoots a thin laser beam in the vertically upward direction. If after refraction from the liquid surface, the laser beam moves along the surface of the liquid, then what is the refrctive index of the liquid ?
View SolutionTwo very large open tanks A&F both contain the same liquid. A horizontal pipe BCD, having a small constriction at C, leads out of the bottom of tank A, and a vertical pipe E containing air opens into the constriction at C and dips into the liquid in tank F. Assume stremline flow and no viscosity. If the cross section area at C is one-half that at D, and if D is at distance h1 below the level of the liquid in A, to what height h2 will liquid rise in pipe E? Express your answer in terms of h1.
[Neglect changes in atmosphere pressure with elevation. In the containers there is atmosphere above the water surface and D is also open to atmosphere.]

View SolutionAn under water swimmer is at a depth of 12 m below the surface of water. A bird is at a height of 18 m from the surface of water, directly above his eyes. For the swimmer the bird appears to be at a distance from the surface of water equal to (Refractive Index of water is 4/3)
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is

View SolutionA liquid is filled in a vessel and a hole is made at a depth h below the free surface of the liquid.
Statement-1 : Greater is the distance of the hole form the free surface of liquid, greater will be the velocity of efflux.
And
Statement-2 The speed of the liquid coming out of the orifice depends on the quantity of liquid in the vessel.
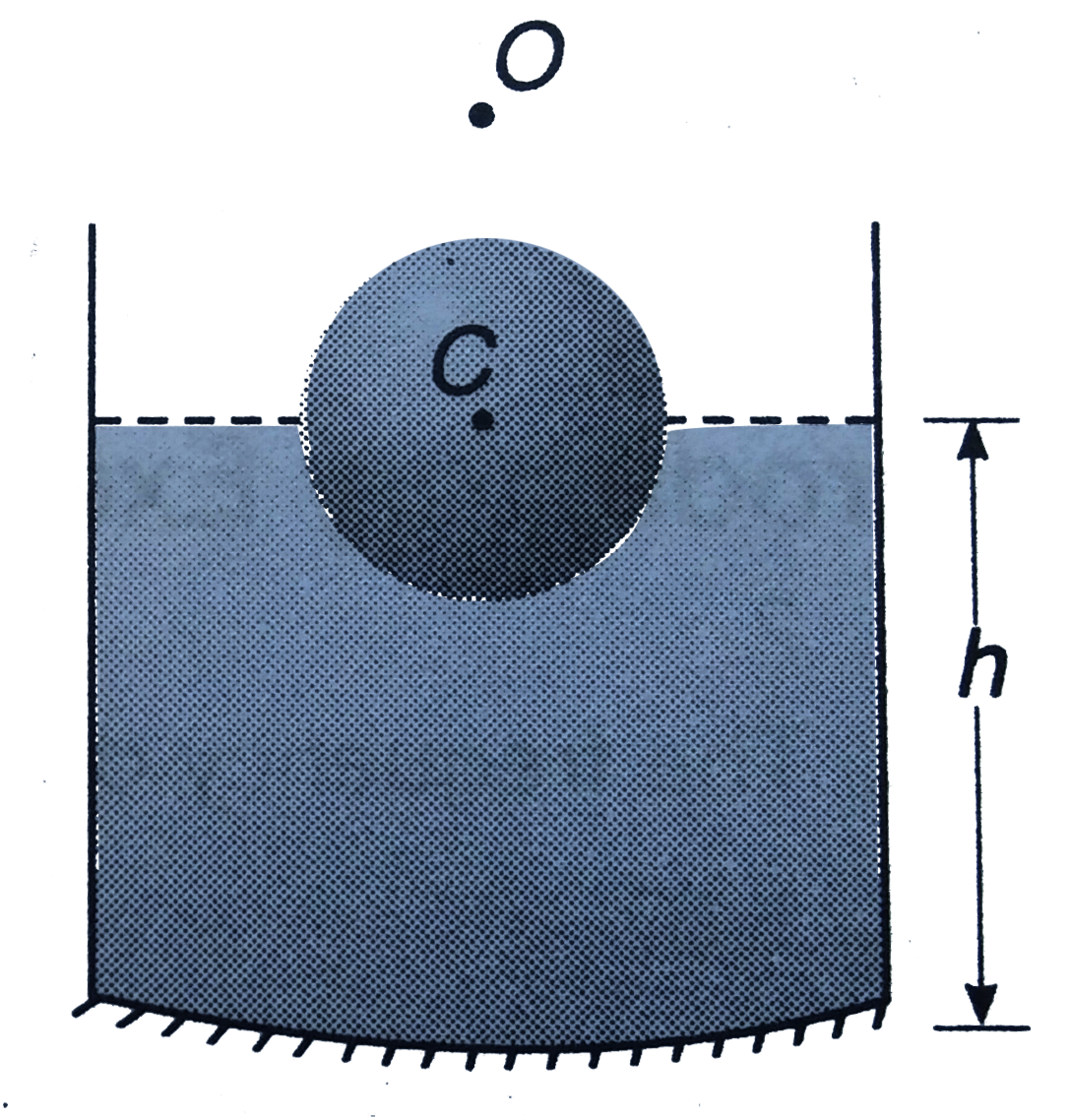
View SolutionA transparent solid sphere of radius 2cm and density ρ floats in a transparent liquid of density 2ρ kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3/2 and that of the liquid is 4/3.
View SolutionA bird is flying up at an angle sin−1(3/5) with the horizontal. A fish in a pond looks at that bird when it is vertically above the fish. The angle at which the bird appears to fly (to the fish) is [μw=4/3]
View Solution
