A bird moves with velocity 20ms−1 in a direction making an angle of 60∘ with the eastern line and 60∘ with vertical upward .Represent the velocity vector in a rectangular form.
To represent the velocity vector of the bird in rectangular form, we will follow these steps:
Step 1: Understand the given information
The bird moves with a velocity of 20m/s at an angle of 60∘ with the eastern line (x-axis) and 60∘ with the vertical upward (y-axis). We need to find the components of this velocity vector in a three-dimensional coordinate system.
Step 2: Define the angles
Let:
- α be the angle with the x-axis (eastern line), which is 60∘.
- β be the angle with the y-axis (vertical), which is also 60∘.
- γ be the angle with the z-axis (the axis perpendicular to the x-y plane), which we need to find.
Step 3: Use the relationship between angles
We know that:
cos2α+cos2β+cos2γ=1
Substituting the known values:
cos2(60∘)+cos2(60∘)+cos2(γ)=1
Calculating cos(60∘):
cos(60∘)=12⟹cos2(60∘)=(12)2=14
Thus, we have:
14+14+cos2(γ)=1
This simplifies to:
12+cos2(γ)=1
So,
cos2(γ)=12
Taking the square root gives:
cos(γ)=±1√2⟹γ=45∘
Step 4: Calculate the components of the velocity vector
Now that we have all angles, we can express the velocity vector →v in rectangular form:
→v=v⋅(cosα^i+cosβ^j+cosγ^k)
Substituting v=20m/s:
→v=20⋅(cos(60∘)^i+cos(60∘)^j+cos(45∘)^k)
Calculating the cosines:
→v=20⋅(12^i+12^j+1√2^k)
Now, multiplying through by 20:
→v=10^i+10^j+20⋅1√2^k
Calculating 20⋅1√2:
20⋅1√2=10√2
Thus, the final velocity vector in rectangular form is:
→v=10^i+10^j+10√2^k
Summary of the solution
The velocity vector of the bird in rectangular form is:
→v=10^i+10^j+10√2^k
The bird moves with a velocity of 20m/s at an angle of 60∘ with the eastern line (x-axis) and 60∘ with the vertical upward (y-axis). We need to find the components of this velocity vector in a three-dimensional coordinate system.
Let:
- α be the angle with the x-axis (eastern line), which is 60∘.
- β be the angle with the y-axis (vertical), which is also 60∘.
- γ be the angle with the z-axis (the axis perpendicular to the x-y plane), which we need to find.
We know that:
cos2α+cos2β+cos2γ=1
Substituting the known values:
cos2(60∘)+cos2(60∘)+cos2(γ)=1
Calculating cos(60∘):
cos(60∘)=12⟹cos2(60∘)=(12)2=14
Thus, we have:
14+14+cos2(γ)=1
This simplifies to:
12+cos2(γ)=1
So,
cos2(γ)=12
Taking the square root gives:
cos(γ)=±1√2⟹γ=45∘
Now that we have all angles, we can express the velocity vector →v in rectangular form:
→v=v⋅(cosα^i+cosβ^j+cosγ^k)
Substituting v=20m/s:
→v=20⋅(cos(60∘)^i+cos(60∘)^j+cos(45∘)^k)
Calculating the cosines:
→v=20⋅(12^i+12^j+1√2^k)
Now, multiplying through by 20:
→v=10^i+10^j+20⋅1√2^k
Calculating 20⋅1√2:
20⋅1√2=10√2
Thus, the final velocity vector in rectangular form is:
→v=10^i+10^j+10√2^k
The velocity vector of the bird in rectangular form is:
→v=10^i+10^j+10√2^k
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.1
19 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.2
13 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
A body is projected with a velocity of 20ms−1 in a direction making an angle of 60∘ with the horizontal. Determine its (i) position after 0.5 s and (ii) the velocity after 0.5s.
View SolutionA beam of protons enters a uniform magnetic field of 0.3T with velocity of 4×105m/s in a direction making an angle of 60∘ with the direction of magnetic field. The path of motion of the particle will be
View SolutionA body is thrown with the velocity 20ms−1 at an angle of 60∘ with the horizontal. Find the time gap between the two positions of the body where the velocity of the body makes an angle of 30∘ with horizontal.
View SolutionA body is thrown into air with a velocity 5 m/s making an angle 30∘ with the horizontal .If the vertical component of the velocity is 5 m/s what is the velocity of the body ? Also find the horizontal component .
View SolutionA particle is projected from a point O with velocity u in a direction making an angle α upward with the horizontal. AT P , it is moving at right angles to its initial direction of projection . Its velocity at P is .
View SolutionA projectile is thrown with a velocity of 20 m/s, at an angle of 60∘ with the horizontal. After how much time the velocity vector will make an angle of 45∘ with the horizontal (in upward direction) is (take g=10m/s2)−
View SolutionA particle is projected upwards with a velocity of 100m/s at an angle of 60∘ with the vertical. Find the time when the particle will move perpendicular to its initial direction, taking g=10m/s2.
View SolutionA ball is projected with a velocity 20√3ms−1 at angle 60∘ to the horizontal. The time interval after which the velocity vector will make an angle 30∘ to the horizontal is (Take, g=10ms−2)
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
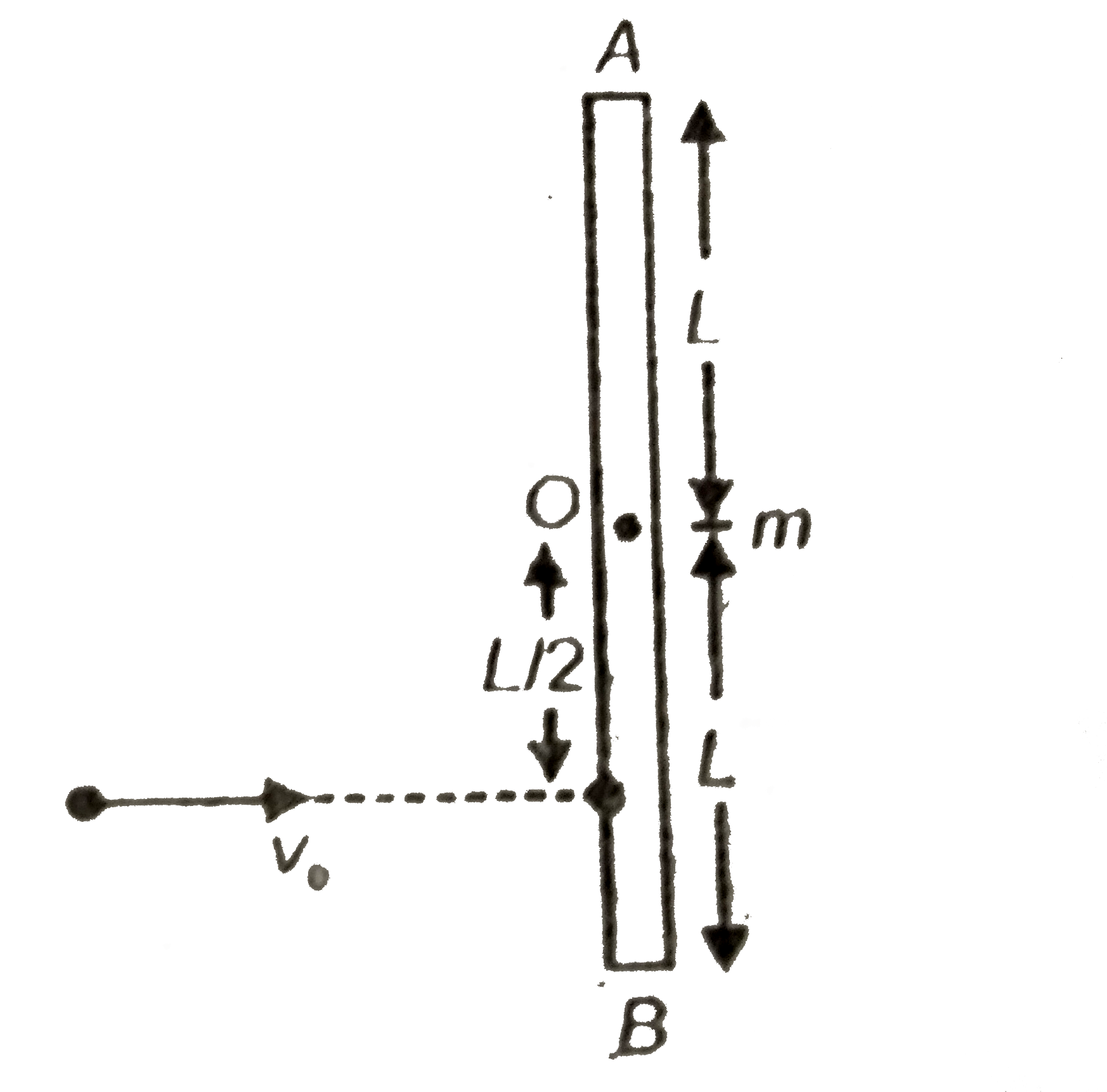
Distance of point P on rod from B which is at rest immediately afte collision is
View SolutionA projectile is thrown in the upward direction making an angle of 60∘ with the horizontal direction with a velocity of 150ms−1. Then the time after which its inclination with the horizontal is 45∘ is
View Solution
